: Suma długości wszystkich krawędzi ostrosłupa prawidłowego
trójkątnego wynosi 72. Krawędź boczna tworzy z podstawą kąt, którego kosinus równy jest
pierwiastek z 3 przez 9. Oblicz pole powierzchni bocznej ostrosłupa .
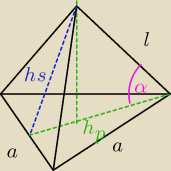3a + 3l = 72
| √3 | ||||||||
= cosα = | |||||||||
| l | 9 |
| a√3 | 2 | 2 | a√3 | a√3 | ||||||
hp = | to | hp = | * | = | ||||||
| 2 | 3 | 3 | 2 | 3 |
| √3 | ||||||||
= | → 3a = l | ||||||||
| l | 3 |
| l | ||
a = | = 6 | |
| 3 |
| 3 | ||
Pb = | *a*hs = 27√35 | |
| 2 |
