Znajdź punkt symetryczny do A(3,-4) względem prostej x - 3*y = 5 . pomocyyy: czesc, prosze was o pomoc. nieco podbramkowa sytuacja Znajdź punkt symetryczny do A(3,−4) względem prostej x − 3*y = 5 . i takie o: Napisz równanie okręgu przechodzącego przez punkty A(0,0), B(3,0), C(2,1) .

pomocyyy: ludzie, pomóżcie

Nienor: p: x−3y−5=0 A(3,−4)

	|3*1+(−3)*(−4)−5|
d=		=√5 → odległość A od prostej p
	12+(−3)2

v=[1,−3] jest prostopadły do prostej p, a więc równoległy do prostej przechodzącej przez A i punkt do niego symetryczny: [x,y]=[3,−4]+t[1,−3] x=3+t ⇒ t=x−3 y=−4−3t y=−4−3(x−3) l: y=−3x+5 → prosta prostopadła do p przechodząca przez A Odległość punktu symetrycznego do prostej jest równa odległości A, a punkt symetryczny ma współrzędne C(x,−3x+5)

	|3*x−3(−3x+5)−5|
√5=
	√5

Wyliczyć x. 2. Podstawić punkty do równania okręgu i wyliczyć.

pomocyyy: dzięki za 1 zadanei, ale gdyby 2 było dla mnie takie proste to bym go nie wrzucał tutaj. ma ktoś ambitniejsze podejście?

sushi_ gg6397228: gotowca możesz sobie przed lekcja przepisać, efekt bedzie taki sam−−> dalej nic nie bedziesz umiec

pomocyyy: nie chce gotowca, ale znam równanie okręgu i nie wiem gdzie tam wstawić 3 punkty. nie wiem jak to rozwiązać.

aniabb: (0−a)²+(0−b)²=r² (3−a)²+(0−b)²=r² (2−a)²+(1−b)²=r² a²+b²=(3−a)²+b² a²=9−6a+a² 6a=9 a=3/2 a²+b²=(2−a)²+(1−b)² 9/4+b²=1/4+(1−b)² policz b potem policz r

pomocyyy: i teraz mam podstawy by to przeanalizować i zrozumieć. dziękuję

Tabek: Nienor czy mógłbyś jednak wyliczyć te działanko i znależć X ? Powinno wyjśc x = 1 a mi za cholere nie wychodzi tyle

Tabek: Również potrzebuje tego zadania oto właściwa treść jak i odpowiedz do niego Znajdź punkt symetryczny do A(3,−4) względem prostej x − 3*y = 5 . odp: P(1,2)

aniabb: d=√10

aniabb:

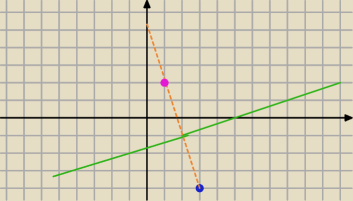
aniabb:

	| x−3(−3x+5)−5|
i w module		=√10 i wychodzi x=1
	√10

Mila: x−3y=5 3y=x−5

	1		5
m: y=		x−
	3		3

Prostopadła do m i A∊k K: y=−3x+b ; −4=−3*3+b⇔b=5 k: y=−3x+5 znajdujemy wsp. punktu przecięcia prostych mi k

1		5
	x−		=−3x+5 ⇔10x=20
3		3

x=2 i y=−3*2+5=−1

	p1+3		p2+(−4)
S jest środkiem odcinka PA⇔2=(		) i −1=		⇔
	2		2

p₁+3=4 i p₂−4=−2⇔p₁=1 i p₂=2

	1		5
P=(1;2) sym. do A=(3;−4) względem y=		x−
	3		3

Mila: Równanie okręgu już masz? ?

tomek: może ktoś to zadanie z okręgiem bardziej rozpisać?