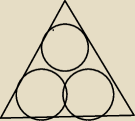
 Na rysunku przedstawiono trójkąt równoboczny i trzy okręgi parami styczne zewnętrznie i
jednocześnie każdy z nich jest styczny do dwóch boków trójkąta. Oblicz pole trójkąta
równobocznego, jeśli promień każdego z okręgów ma długość 1 cm.
Na rysunku przedstawiono trójkąt równoboczny i trzy okręgi parami styczne zewnętrznie i
jednocześnie każdy z nich jest styczny do dwóch boków trójkąta. Oblicz pole trójkąta
równobocznego, jeśli promień każdego z okręgów ma długość 1 cm.
| 2 | ||
(2+ | ) | |
| tg30o |
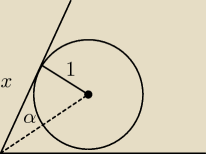 α=30 bok Δ = 2x+2
α=30 bok Δ = 2x+2
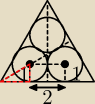 wysokość poprowadzona z wierzchołka przechodzi przez środek okręgu, tworzy trójkąt (30, 60 ,90)
[na rysunku to ten trójkąt obrysowany na czerwono], którego najkrótszy bok ma długość 1, nas
interesuje natomiast średni bok, który stanowi część podstawy, ma on √3
zatem cały bok trójkąta
a = √3 + 2 + √3 = 2√3 + 2
no to tylko podstawić na pole trójkąta.
wysokość poprowadzona z wierzchołka przechodzi przez środek okręgu, tworzy trójkąt (30, 60 ,90)
[na rysunku to ten trójkąt obrysowany na czerwono], którego najkrótszy bok ma długość 1, nas
interesuje natomiast średni bok, który stanowi część podstawy, ma on √3
zatem cały bok trójkąta
a = √3 + 2 + √3 = 2√3 + 2
no to tylko podstawić na pole trójkąta.