witam zvidek: Mam za zadanie wyznaczyć dziedzinę funkcji g(x) = arcsin √3x założyłem że x ≥ 0 , √3x ≥ −1 i √3x≤1 wyszło mi że x ≥ ¹₃ i x ≤ ¹₃ w odpowiedziach mam że x ∊ <0, ¹₃ > nie wiem gdzie popełniam błąd. Prosze o pomoc

Nienor: √3x≥−1 spełnione w całej dziedzinie. Nie można czegoś takiego podnosić do kwadratu i sobie rozwiązywać, to jakbyś miał |3x|≥−1. Chyba tu masz błąd.

:): pamiętaj o założeniu, że wyrażenie pod pierwiastkiem musi być >=0 czyli: 3x>=0 z czego dostajemy że x>=0 i później częśc wspólna z tym co już masz

:): wg mnie można podnosić, bo pierwiastek kwadratowy może być tylko z liczb nieujemnych (jeżeli nie mówimy o l.zespolonych)

Nienor: 3x≥1

	1
x≥		wychodzi po podniesienu, co jest bzdurą, bo:
	3

√0≥−1 Żeby podnosić do kwadratu takie wyrażenie musimy założyć, że obie strony są nieujemne.

zvidek: no nie chodzi mi o liczby zespolone

:): ok, racja czyli prościej by było napisać założenie, że pierwiastek jest zawsze nieujemny przez co już wiemy, że musimy rozpatrywać nierówność w przedziale <0;1> (dla funkcji arcsin) i teraz już możemy podnosić do kwadratu, taki sposób jest dobry?

Nienor: No to już wiadomo co zrobiłeś źle. Ma być: √3≥−1, dla x∊[0;+∞)

	1
√3≤1, dla x∊[0;		)
	3

Aga1.: Ogólnie g(x)=arcsin√3x −1≤√3x≤1 ale √3x≥0 więc 0≤√3x≤1 podnieś do kwadratu 0≤3x≤1 /:3

	1		1
0≤x≤		, czyli x∊<0,		>
	3		3

:): dokładnie o takie coś jak napisała Aga mi chodziło

zvidek: Aga1 nie rozumiem dlaczego √3x musi być większe boć równe zeru. może mi ktoś to wytłumaczyć?

Aga1.: Dokładniej to 3x≥0 √a=b⇔(b²=a i a≥0 i b≥0)−−to jest definicja pierwiastka arytmetycznego.

:): po prostu pierwiastek kwadratowy musi być z liczby dodatniej, bądź równej zero. w zbiorze liczb rzeczywistych nie istnieje np √−2 albo √−1 czy jakikolwiek inny z liczby ujemnej

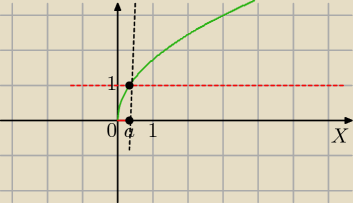
Mila: y=p{3x) wykres zielony D=<0;a> trzeba rozwiązać równianie √3x=1

	1
x=
	3

	1
x∊<0;		>
	3