:)) Maslanek: Geometria, planimetria i inne dowody lub wywody Mógłbym prosić jakieś zadanka do puknięcia? Tylko bez szału, tak żebym miał szansę zrobić To moja pięta Achillesowa, więc trzeba by trochę podziałać z tym, skoro mam odrobinę czasu. Dziękuję

Ajtek: No to już, niby trygonometria, ale jednak nie do końca: Udowodnij że: sin²x+cos²x=1 .

Mila: Maslanek, jaki poziom?

Maslanek: LO

Maslanek:

	y
sinx=
	r

	x
cosx=
	r

	y2		x2		x2+y2		r2
sin2x+cos2x=		+		=		=		=1.
	r2		r2		r2		r2

Ajtek: Przez ukłąd współrzędnych polazłeś . A w Δ prostokątnym?

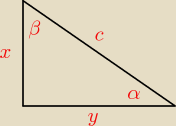
Maslanek: β=π/2−α x²+y²=c²

	x
sinα=
	c

	y
cosα=
	c

Dokładnie tak samo . Zresztą to czysta analogia do układu współrzędnych

Ajtek: Phi, cfaniak .

Mila: Dla Maslanka: 1)2sin²x−2sin²xcosx=1−cosx 2) tgx=2

	π
x∊(0;		)
	2

uzasadnij, że cosx jest liczbą niewymierną

Maslanek: 1) 2sin²x(1−cosx)−(1−cosx)=0 (1−cosx)(2sin²x−1)=0 cosx=1 lub sinx=√2/2 lub sinx=−√2/2 x=2kπ lub x=π/4+2kπ lub x=3π/4+2kπ lub x=7π/4+2kπ lub x=5π/4+2kπ. 2) tgx=2 ⇒ sinx=2cosx sin²x+cos²x=1 Czyli: 5cos²x=1

	√5
cosx=		.
	5

Ale ja chcę geometrię . Algebra to śmiga

ZKS: A gdzie dowód niewymierności?

Maslanek: Słuszna uwaga

	√5		m
Załóżmy, że		=		, gdzie NWD(m,n)=1 oraz m,n∊C
	5		n

	5m
√5=
	n

	25m2
5=
	n2

5n²=25m² n²=5m² Eee... i co dalej? xD

ZKS:

n2
	= 5 a jak wiesz 5 jest liczbą pierwszą i dzieli się przez 1 lub 5 więc mamy
m2

sprzeczność ponieważ kwadrat żadnej liczby wymiernej nie da liczby 5.

ZKS: Coś tam sknociłem ale mam nadzieję że mniej więcej wiesz o co chodzi.

Mila: Dla Maslanka: Pole powierzchni podstawy graniastosłupa prostego trójkątnego wynosi P. Przez krawędź podstawy tej bryły poprowadzono płaszczyznę, która przecina przeciwległą krawędź boczną i jest nachylona do płaszczyzny podstawy pod kątem α=U{π}4. Oblicz pole otrzymanego przekroju.

Maslanek: Brrr... Ale bez stereometrii

Ajtek: Mila stereometrii, podobnie jak i trygonometrii nie widzę w treści prośby . To będzie weekend czy środek tygodnia

Maslanek: Ale ogólnie, to chyba

	P		a		b		P		P
P=xysina=		*		*		=		=		=2P
	ab		cos45		cos45		cos245		1/2

Mila: Jutro, będą ładne zadanka z planimetrii.:Maslanek−inny wynik. Ajtek nie wiem. Dobranoc dla sympatycznych forumowiczów.

Maslanek: W ogóle nie rozumiem jak może przecinać przeciwległą krawędź boczną Skoro przechodzi przez jedną z krawędzi podstawy, to naprzeciw niej jest przecież kanciasta ściana (tj. złożenie dwóch ścian)

Basiek: Bry, Maslanek− gdybyś chciał jakieś fajne planimetryczne dowodziki, to jakieś tam mam. Ale od razu mówię, że do rozwiązań ani się nie wtrącam, ani nie mam zamiaru nawet tego dotykać.

Maslanek: To rzuć no, Basieńko Zobaczymy co to warte Witam serdecznie po dłuuuuuugim czasie Zapomniałem, że istniejesz już

Mila: Zadania dla Maslanka i Saizou 1) Dane są dwa boki a i b trójkąta ABC Znaleźć bok c, jeśli wiadomo,że kąt C jest dwa razy większy od kąta B. 2) Pole trójkąta prostokątnego wynosi 600cm², zaś stosunek przeciwprostokątnej do jednej z przyprostokątnych jest równy 5:4. Oblicz obwód tego trójkąta. 3) Znaleźć pole trójkąta mając dany jego bok i dwa kąty do niego przyległe. 4) Znaleźć wysokość trójkąta równoramiennego polu równym 3√3 wpisanego w okrąg o promieniu 2.

Mila: ?

aniabb: https://matematykaszkolna.pl/forum/167760.html

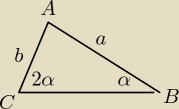
Maslanek: Z twierdzenia sinusów:

sin x		sin 2x		2sinx cosx
	=		=
b		a		a

	1		2 cos x
Stąd		=
	b		a

	a
b=
	2 cos x

	a
cos x =
	2b

c²=a²+b²−2ab*cos(180−3x)=a²+b²−2ab(cos180cos3x+sin180sin3x) c²=a²+b²+2ab*cos3x=a²+b²+2ab*(4cos³x−3cosx)

	a3		3a
c2=a2+b2+2ab*(		−		)
	2b2		2b

	a4
c2=a2+b2+		−3a2
	b

c²=U{a⁴}+b²−2a². Ciekawe czy dobrze

Basiek: 1) W trójkącie ABC przez dowolny punkt A' środkowej AD prowadzimy równolegle do boku AB prostą przecinającą bok BC w punkcie B', a równolegle do boku CA prowadzimy prostą przecinającą bok BC w punkcie C'. Wykaż, że A'D jest środkową trójkąta A'B'C'. 2) W równoległoboku ABCD punkty K i L są środkami boków AB i AD. Wykaż, że odcinki CK i CL dzielą przekątną BD tego równoległoboku na trzy równe odcinki. 3) Dwa okręgi o środkach S₁ i S₂ przecinają się w punktach A i B, przy czym punkty S₁ i S₂ leżą po przeciwnych stronach prostej AB. Miary kątów AS₁B i AS₂B wynoszą odpowiednio 90^o i 60^o. Wyznacz długości promieni tych okręgów wiedząc, że |S₁S₂|=a 4) Mając dany wielokąt wpisany w okrąg, tworzymy nowy wielokąt o podwójnej liczbie wierzchołków, dołączając do danych wierzchołków punkty połowiące łuki okręgu zawarte między kolejnymi wierzchołkami danego wielokąta. Wykaż, że pole nowego wielokąta jest równe połowie iloczynu obwodu danego wielokąta przez długość promienia okręgu. Przepraszam.... zagapiłam się, dlatego nie wkleiłam wcześniej. Tak, czasem też zapominam, że istnieję. Powodzenia.

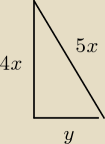
Maslanek: P=2x*y y²=25x²−16x²=9x² ⇒ y=3x Wtedy P=2x*3x=6x²=600 ⇒ x=10 (cm). L=30+40+50=120cm

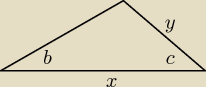
Maslanek: Z twierdzenia sinusów:

y		x		x
	=		=
sin b		sin(180−(b+c)		sin(b+c)

	x*sin b
Wtedy: y=
	sin(b+c

	1		1		sin b*sin c*x
Wtedy: P=		xy sin c =		*x*
	2		2		sin b*cos c + sin c*cos b

	1		1
P=		*x2*
	2		ctg c+ctg b

Maslanek: Na czwarte nie mam siły już Na takie przygotowany nie jestem

Mila: 1) c=√b(a+b) sprawdz przekształcenia, prościej, gdybyś poprowadził dwusieczną kąta C i skorzystał z własności dwusiecznej. 2)120cm dobrze 3)dobrze.

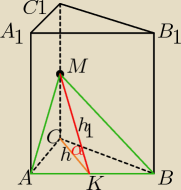Mila: Dla Maslanka Odnośnie zadania ze stereometrii z godziny 23:56. Rysunek: ΔABM to właśnie ten przekrój. α=45⁰