Zadanie z przekształcania funkcji. MP. : Witam! Niedługo zbliża mi się kolokwium a jednym z tematów w nim zawartych będzie rysowanie funkcji i ich przekształcanie. Liniowych i kwadratowych, wykładniczych i logarytmicznych oraz trygonometrycznych. Może znalazła by się tu miła osoba i zechciałaby mi pomóc w przekształcaniu wykresów funkcji? Chodzi mi głównie o kolejność przekształcania wykresów bo to sprawia mi największą trudność i właściwie poprostu tego nie umiem. Wiem, że jeżeli przekształcam np. e^1−x to najpierw rysuję sobie wykres funkcji wykładniczej e^x a potem przekształcam. Wiem co robi znak − przed x i przed całą funkcją. Wiem co robi wartość bezwzględna oraz znam przesunięcie w lewo i w górę. Niestety niewiem co z kolejnością i jak to rozpoznawać. Może jest jakiś sposób bądź schemat ( a właściwie to przypuszczam, że napewno jest.) , który mówi co najpierw robimy. Dla przykładu: a) y = |x² − 4| + 3 b) e^1−|x| c) y = |sinx −2| d) 2^−x+3 e) y = |e^x − 3| f) 1 − e^1−|x| Nie chcę, żebyście mi rysowali, gdyż wiem jak to będzie wyglądać na końcu po przekształceniu. Prosiłbym natomiast o wyjaśnienie co w jakiej kolejnośći i dlaczego tak. Jaką przyjąć uniwersalną metodą robienie tego. Pozdrawiam!

MP. : Pomozecie?

zośka: a) y=x² → o 4jednostki w dół (translacja o wektor [0,−4]) y=x²−4 →to co znajduje się pod osią x, odbijamy symetrycznie do góry wzgl. osi x y=|x²−4| → przesuwamy o 3 jednostki w górę (translacja o wektor [0,3]) mamy y=|x²−4| +3

Trivial: Nie ma uniwersalnego schematu. Zazwyczaj najlepiej jest zacząć od funkcji najbardziej zagnieżdżonych.

MP. : njabardziej zagnieżdżonych , tzn.? Nie ma sposobu ale jakoś trzeba to ogarniać na kolokwium..

MP. : zośka, dziękuje za pierwsze. Może ktoś by spróbował z resztą?

zośka: b) ja bym zrobiła to tak: zauważ, że dla x≤0 funkcja ta ma postać: y=e^1+x Wykres ten można uzyskać przesuwając y=e^x o wektor [−1,0] czyli o 1 w lewo. Bierzemy zaznaczamy tę część wykresu, gdzie x<0 . Odbijamy ją wzgl. osi y i mamy wykres dla x≥0

zośka: c) y=sinx →translacja o wektor [0,−2] ( o 2 w dół) y=sinx−2 → część wykresu znajdującą się pod osią x odbijamy symetrycznie wzgl. osi x do góry y=|sinx−2|

Trivial: Najbardziej zagnieżdżone, czyli te, które "wykonujesz jako pierwsze", żeby obliczyć wartość wyrażenia dla jakiegoś x. Będą to kolejno: a) x² b) |x| c) sin(x) d) −x e) e^x Na zielono zaznaczyłem te przykłady, dla których rzeczywiście warto wyjść od tych funkcji. Jak widać, gdy mamy nietrywialne eksponenty wskazówka się nie sprawdza.

Trivial: Aha, jeszcze zabrakło f) |x|

zośka:

	1
d) y=2−x+3=2−(x−3)=(		)x−3
	2

	1
rysujemy y=(		)x →przesuwamy o wektor [3,0] (o 3 w prawo)
	2

MP. : dziękuje. Będe ćwiczył. Trivial a co to znaczy nietrywialne eksponenty?

Trivial: Np. 2^x, 3^x, 7^x, e^x to "trywialne eksponenty". Ale już e^1−|x| tak trywialne nie jest. Te zadania są na wyczucie. Przerób trochę przykładów, to też będziesz wiedział od czego warto zacząć. Powodzenia!

MP. : a może podałbyś mi kilka przykładów? Ale tak od łatwiejszych z 3,4 do średnich z 3,4 a potem trudne z 3,4 ( no nie trudniejsze od tych co podałem ja) A ja sobie na wolframie będe sprawdzał czy wyszło ok.

MP. : Jeszcze takie dwie, nie wydające się być trudnymi. y = lnx² oraz y = ln²x Niewiem jak kwadraty wpływają na wykres funkcji..

Trivial: Do pierwszego: ln(x²) = 2*ln(|x|) Do drugiego: narysuj ln(x) i potem podnoś wartości do kwadratu dla wybranych punktów. Połącz kropki. Chyba innej metody nie ma. ;>

MP. : 2ln(|x|) a 2 z przodu co nam daje?

Trivial: Mnożymy razy dwa każdą wartość. (skalujemy wykres)

MP. : ahaaa. I teraz. Najpierw zrobimy wartość bzwzgl. czy najpierw zeskalujemy? I takie o to pytania mi chodzą po głowie. No nic, podaj mi kilka fajnych przykładów a ja popróbuję porozwiązywać.

Trivial: Ok. Lista zadań: 1) sin(x+3) + 5 2) 2e^x−5 3) ln(e^x2+4x−2) 4) sin(3−|x+3|)

	1
5)		|cos(1−|x|)|
	2

6*) |sin(x) + cos(x)|

MP. : ojoj Daj mi najpierw coś łatwiejszego, żebym się wprawił Bo widzę, że dosyć ostre dałeś.

Trivial: Pierwsze są proste. Potem coraz trudniejsze.

Trivial: Ale skoro chcesz więcej prostych to masz:

	π
7) tg(x+		)
	2

8) (x+3)³ − 5 9) x² − 2|x| + 3 Wskazówka: x² = (|x|)² 10) e^−|x| 11) 2^1−2x

MP. : no i tak. Pierwsze zrobiłem. Drugie zrobiłem do e^x−5 a nie umiem zeskalować...

MP. : o proste. Tak Od tego zacznę lepiej

MP. : ale tam znowu pojawia się (x+3)³ a ja niewiem co z tym sześcianem.

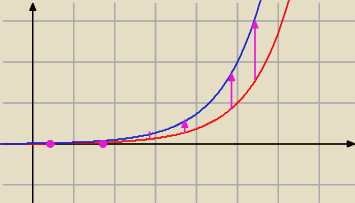
Trivial: Wybierz sobie parę punktów odniesienia i zeskaluj je dokładnie. Przez otrzymane punkty poprowadź krzywą.

Trivial: 8) wyjdź z funkcji x³. Zrób translację o odpowiedni wektor i koniec zadania.

MP. : czyli czy dobrze rozumiem Twój wykres? Jeżeli miałem funkcje założym, gdzie dla x = 2 y = 5, dla x = 3 y = 6 to teraz dla x = 2 bede miał y = 25 a dla x = 3 y = 36, tak?

Trivial: Ten wykres jest do pytania o 2*e^x−5.

MP. : no tak ale tu jest skalowanie.

Trivial: Skalowanie jest o stały czynnik, czyli np. wybraliśmy punkty: (0, e⁻⁵) → (0, 2*e⁻⁵) (1, e⁻⁴) → (1, 2*e⁻⁴) (2, e⁻³) → (1, 2*e⁻³) (3, e⁻²) → (1, 2*e⁻²) (4, e⁻¹) → (1, 2*e⁻¹) (5, 1) → (1, 2) (6, e) → (1, 2*e) ...

Trivial: Ahh.. Za dużo kopiowania. Po prawej wszędzie powinno być takie samo x jak po lewej, czyli 0, 1, 2, ..., 6