Kilka zadań z planimetrii Artur: 1) Dany jest trójkąt ABC, w którym kąt BCA= 900 a kąt CAB jest dwa razy mniejszy od kąta CBA. Obwód okręgu wpisanego w ten trójkąt wynosi 2π. Prosta przechodząca przez wierzchołek C danego trójkąta tworzy z krótszą przyprostokątną kąt o mierze 30 stopni i przecina przeciwprostokątną AB w punkcie D. a) Oblicz pole koła opisanego na danym trójkącie oraz wyznacz stosunek długości odcinka DB do długości odcinka DA. b) Oblicz odległość punktu D od środka okręgu wpisanego w trójkąt ABC. 2) W trójkącie ABC dane są współrzędne wierzchołków A i B, gdzie A = (−1,−1) i B = (7,1) oraz równanie symetralnej boku BC: x – 4y + 14 = 0. Wyznacz współrzędne wierzchołka C oraz wykaż, że trójkąt ABC jest trójkątem prostokątnym. Napisz równanie okręgu opisanego na trójkącie ABC. 3) Środkowe trójkąta prostokątnego poprowadzone z wierzchołków kątów ostrych mają długości 5 i √40. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim. Oblicz długość środkowej trójkąta poprowadzonej z wierzchołka kąta prostego. 4) Promień koła opisanego na trójkącie prostokątnym jest 2,5 razy większy od promienia koła wpisanego w ten trójkąt. a) Wyznacz cosinusy kątów ostrych w tym trójkącie. b) Określ w procentach, jaką część pola trójkąta ABC zajmuje koło wpisane w ten trójkąt. Proszę o pomoc

Artur: pomyłka Kąt BCA = 90 stopni a nie 900

Artur: Da radę ktoś to zrobić?

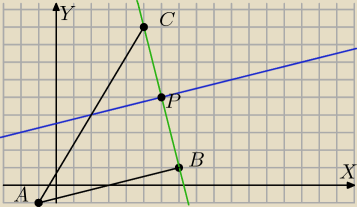
Mila: s: x−4y+14=0 symetralna BC ( niebieska) s⊥BC i przechodzi przez środek BC

	1		7
s: y=		x+
	4		2

bok BC leży na prostopadłej do prostej s prosta BC: y=−4x+b i B∊prostej BC 1=−4*7+b ⇔b=29⇔y=−4x+29 szukam puntu przecięcia z symetralną

	1		7
−4x+29=		x+
	4		2

x=6 to y=−4*6+29=5

	c1+7		c2+1
P=(6;5) to środek BC: stąd 6=		i 5=
	2		2

C=(c₁;c₂)=(5;9) uzasadnij, że Δjest prostokątny ( np. z tw. odwrotnego do tw. Pitagorasa) środek okręgu będzie leżał w środku boku AC A = (−1,−1) i B = (7,1), C=(5;9) S=(2;4) r=√3²+5² dokończ. (x−2)²+(y−4)²=r²

Artur: Dziękuję

Artur: Jest problem z dowodem ze trójkąt jest prostokątny, mogłabyś sprawdzić czy wszystko się zgadza w Twoich obliczeniach?

Artur: Pomo że ktoś z 3?

Artur: Pomoże*

Artur: Poradziłem sobie, jeszcze 4 tylko prosze

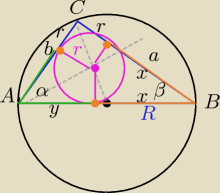
Mila: 4) R=2,5r Punkty styczności są jednakowo odległe od wierzchołka kąta. c=x+y=2R=5r a+b=2r+x+y a+b=2r+5r=7r a²+b²=25r² a=7r−b (7r−b)²+b²=25r² po rozwinięciu i redukcji b²−7rb+12r⁼0 Δ=r² b=4r i a=3r

	b		4r		4
cosα=		=		=
	c		5r		5

	3
cosβ=
	5

Artur: Bardzo dziękuję