Dla Oli Tadeusz:

krystek: I czego Ola oczekuje?

Tadeusz: Zadanie to możemy rozwiązać na kilka sposobów ... 1. Wiemy, że r=2R

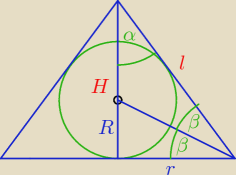
	R		R		1
zatem tgβ=		=		=
	r		2R		2

	2tgβ		1		4
tg2β=		... zatem tg2β=		=
	1−tg2β		1   1−   4		3

α=90−2β

	4
zatem ctgα=tg2β=
	3

Znając ctgα ... policzymy cosα (przy załozeniu, że α z pierwszej ćwiartki)

	cosα		cosα		4
ctgα=		=		=
	sinα		√1−cos2α		3

stąd 3cosα=4√1−cos²α 9cos²α=16−16cos²α

	16		4
cos2α=		... dla I ćwiartki cosα=
	25		5

Szukamy cos2α ... zatem cos2α=cos²α−sin²α=2cos²α−1

	16		32		7
cos2α=2*		−1=		−1=
	25		25		25

	7
cos2α=
	25

Tadeusz: Oczywiście nie jest to jedyny sposób.

	r
Znając tg2β możemy (patrz wyżej) możemy wyznaczyć		=sin2β ... l=
	l

Tadeusz:

	r		r
Oczywiście		=cos2α... l=
	l		cos2β

	4
Skoro tg2β=
	3

sin2β		√1−cos22β		4
	=		=		... 3√1−cos22β=4cos2β
cos2β		cos2β		3

9−9cos²2β=16cos²2β 9=25cos²2β

	3
przy założeniu, że 2β jest z pierwszej ćwiartki cos2β=
	5

	5
zatem l=		r
	3

Teraz możemy sięgnąć po twierdzenie cosinusów (2r)²=l²+l²−2l*lcos2α

	25		25
4r2=2		r2−2		r2cos2α
	9		9

50		50		50		14		14		7
	cos2α=		−4 ...		cos2α=		... cos2α=		=
9		9		9		9		50		25

Tadeusz:

	H
Trzeci sposób to policzenie również H i potem wyznaczenie cosα jako
	l

Znając cosα ...wyznaczymy cos2α jak w sposobie pierwszym jak widzisz ... do wyboru ... do koloru−

MQ: Pod warunkiem, że jest on czerwony

Tadeusz: ... to tak jak czarny u Forda −