funkcje odwrotne piórnik: Wyznacz wzory i dziedziny funkcji odwrotnych do funkcji:

	2x−1
a) f(x)=
	3x+2

b) f(x)=2+3^2x−2 c) f(x)=log(2+10^x−1) d) f(x)=1+³√2x−1

Artur_z_miasta_Neptuna: i w czym konkretnie problem ? wiesz jak się wyznacza wzór funkcji odwrotnej

piórnik: właśnie tego nie wiem ...

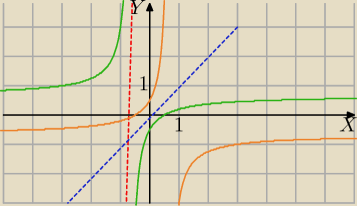
Mila: a)

	2x−1
(*) y=		(zielony wykres)
	3x+2

	2
D=R\{−		}
	3

funkcja odwrotna istnieje dla funkcji różnowartościowej wyznaczam x z wzoru (*) (3x+2)y=2x−1 3xy+2y=2x−1 3xy−2x=−1−2y x(3y−2)=−1−2y

	1+2y
x=
	−3y+2

Zamiana zmiennych

	1+2x
y=		wykres pomarańczowy
	−3x+2

	2
D=R\{
	3

[wykresy są symetryczne względem prostej y=x]

Mila: b) f(x)=2+3^2x−2 D=R y=2+3^2x−2 y−2=3^2x−2 Zał. y−2>0⇔y>2 logarytmujemy obustronnie log₃(y−2)=2x−2 log₃(y−2)+2=2x

	1
x=		log3(y−2)+1
	2

Zmiana zmiennych

	1
y=		log3(x−2)+1
	2

D=(2;∞)

piórnik: powie ktoś jak rozwiązać c?