 Eta bardzo Cie proszę pomóż mi wytłumacz:
mam takie zadania na egzamin z matmy
Eta bardzo Cie proszę pomóż mi wytłumacz:
mam takie zadania na egzamin z matmy Narysuj wykres funkcji:
y = x2(do kwadratu) −6x + 9
zapisz w postaci kanonicznej i odczytaj ZWF
2) Narysuj wykres funkcji
y =3 ( x−2) 2 ( do kwadr) +1
określ przedziały monotoniczności funkcji wskaz wartosc najmniejsza lub najwieksza funkcji.
3) Wyznacz miejsce zerowe funkcji:
y− 3x + 5 =0
oraz wkaz czy funkcja jest roznaca czy malejaca
4 Oblicz odleglosc punktu P(−1, −2) od prostej
y = x+1.
Mam z tym problemy a teraz musze jezdzic na rehabilitacje do poradni na prawie caly dzien
wracamy z mama okolo 15− 16 ( jezdze na wozku) jak wracam to jestem padneta i
wypompowana i mam dosc.
5 oblicz dlugosc odcinka i jego srodek jezeli
A( −4, 2)
B(2, 8)
Sorry, nie jestem mocna w tym a w dodatku rehabilitacja dluzsza musi byc
przez zime wszystko stanelo w miejscu z zdrowkiem( zaczyna mocno szwankowac)
Moze bys weszla na gg o ile bedziesz chciec to porozmiawiamy co?( nastepnym razem to podam)
musze juz konczyc bo musimy jechac.
(egzamin mam 22 maja.
Narysuj wykres funkcji:
y = x2(do kwadratu) −6x + 9
zapisz w postaci kanonicznej i odczytaj ZWF
2) Narysuj wykres funkcji
y =3 ( x−2) 2 ( do kwadr) +1
określ przedziały monotoniczności funkcji wskaz wartosc najmniejsza lub najwieksza funkcji.
3) Wyznacz miejsce zerowe funkcji:
y− 3x + 5 =0
oraz wkaz czy funkcja jest roznaca czy malejaca
4 Oblicz odleglosc punktu P(−1, −2) od prostej
y = x+1.
Mam z tym problemy a teraz musze jezdzic na rehabilitacje do poradni na prawie caly dzien
wracamy z mama okolo 15− 16 ( jezdze na wozku) jak wracam to jestem padneta i
wypompowana i mam dosc.
5 oblicz dlugosc odcinka i jego srodek jezeli
A( −4, 2)
B(2, 8)
Sorry, nie jestem mocna w tym a w dodatku rehabilitacja dluzsza musi byc
przez zime wszystko stanelo w miejscu z zdrowkiem( zaczyna mocno szwankowac)
Moze bys weszla na gg o ile bedziesz chciec to porozmiawiamy co?( nastepnym razem to podam)
musze juz konczyc bo musimy jechac.
(egzamin mam 22 maja.
 Pomogę Ci .......
zad1/ do narysowania wykresu funkcji kwadratowej, której wykresem jest parabola
należy : obliczyć współrzędne wierzchołka W
gdzie : xw= −b2a
yw = −Δ4a
oraz podać miejsca zerowe : x1 i x2
−− należy wiedzieć , jak skierowane są ramiona paraboli.
to zależy od znaku współczynnika "a"
jeżeli a >0 −−− ramiona do góry
jezeli a<0 −−− ramiona do dołu
zbiór wartości to: y€ (−∞, yw> −−− gdy ramiona skierowane do dołu
lub y€ < yw, +∞) −−− gdy ramiona skirowane do góry
postać kanoniczną zapisujemy tak:
y= a( x −xw)2 + yw
( to musisz wiedzieć i zapamiętać, wtedy narysujesz każdy wykres funkcji
kwadratowej
Pomogę Ci .......
zad1/ do narysowania wykresu funkcji kwadratowej, której wykresem jest parabola
należy : obliczyć współrzędne wierzchołka W
gdzie : xw= −b2a
yw = −Δ4a
oraz podać miejsca zerowe : x1 i x2
−− należy wiedzieć , jak skierowane są ramiona paraboli.
to zależy od znaku współczynnika "a"
jeżeli a >0 −−− ramiona do góry
jezeli a<0 −−− ramiona do dołu
zbiór wartości to: y€ (−∞, yw> −−− gdy ramiona skierowane do dołu
lub y€ < yw, +∞) −−− gdy ramiona skirowane do góry
postać kanoniczną zapisujemy tak:
y= a( x −xw)2 + yw
( to musisz wiedzieć i zapamiętać, wtedy narysujesz każdy wykres funkcji
kwadratowej )
tak więc w Twoim przykładzie , widzisz ,że a = 1
Myślę ,że dasz już radę
)
tak więc w Twoim przykładzie , widzisz ,że a = 1
Myślę ,że dasz już radę ( jeżeli nie? ... to pisz ... pomogę)
więc ramiona paraboli skierowane do góry
Zad/ 2
podobnie:
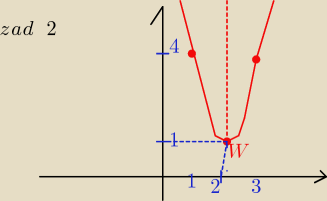
masz już postać kanoniczną: y = 2( x −2)2 + 1
więc W( 2,1) bo xw= 2 yw = 1
ramiona paraboli skierowane są do góry , bo a =3 >0
podaj jeszcze kilka punktów które należą do wykresu:
np: dla x = 1 y= 3( 1 −2)2 + 1 => y= 3*1 +1 => y=4 to:( 1,4)
dla x= 3 y= 3( 3 −2)2 +1 => y= 3*1 +1 => y = 4 to: ( 3,1)
dla x= 2 y= 3( 2−2)2 +1 => y= 3*0 +1 => y= 1 to: ( 2, 1)
itd.....
teraz narysuj tę parabolę.
funkcja osiąga wartość najmniejszą w wierzchołku paraboli ( bo ramiona do góry)
gdy ramiona do dołu : to w wierzchołku jest wartość największa
zatem w Twoim zadaniu :
wartość najmniejsza wynosi yw= 1 dla xw = 2
przedziały monotoniczności to: ( zobaczysz na wykresie)
funkcja maleje dla x€( −∞, xw> => x€( −∞,2>
" " rośnie dla: x€ < xw, +∞) => x€ < 2,+∞)
Za chwilę podam Ci pozostałe rozwiązania
( jeżeli nie? ... to pisz ... pomogę)
więc ramiona paraboli skierowane do góry
Zad/ 2
podobnie:
masz już postać kanoniczną: y = 2( x −2)2 + 1
więc W( 2,1) bo xw= 2 yw = 1
ramiona paraboli skierowane są do góry , bo a =3 >0
podaj jeszcze kilka punktów które należą do wykresu:
np: dla x = 1 y= 3( 1 −2)2 + 1 => y= 3*1 +1 => y=4 to:( 1,4)
dla x= 3 y= 3( 3 −2)2 +1 => y= 3*1 +1 => y = 4 to: ( 3,1)
dla x= 2 y= 3( 2−2)2 +1 => y= 3*0 +1 => y= 1 to: ( 2, 1)
itd.....
teraz narysuj tę parabolę.
funkcja osiąga wartość najmniejszą w wierzchołku paraboli ( bo ramiona do góry)
gdy ramiona do dołu : to w wierzchołku jest wartość największa
zatem w Twoim zadaniu :
wartość najmniejsza wynosi yw= 1 dla xw = 2
przedziały monotoniczności to: ( zobaczysz na wykresie)
funkcja maleje dla x€( −∞, xw> => x€( −∞,2>
" " rośnie dla: x€ < xw, +∞) => x€ < 2,+∞)
Za chwilę podam Ci pozostałe rozwiązania PS: Życzę Ci dużo zdrówka!
Nie przejmuj się, poradzisz sobie napewno
PS: Życzę Ci dużo zdrówka!
Nie przejmuj się, poradzisz sobie napewno
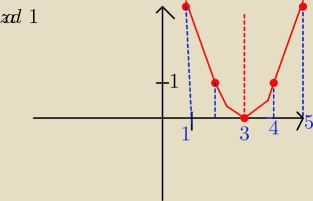 W zad 1/ y = x2 − 6x + 9 = ( x −3)2 więc W( 3,0)
y = ( x−3)2 −−−−−−− to postać kanoniczna.
zb. wart. y€ < 3 , +∞)
W zad 1/ y = x2 − 6x + 9 = ( x −3)2 więc W( 3,0)
y = ( x−3)2 −−−−−−− to postać kanoniczna.
zb. wart. y€ < 3 , +∞)
 ( zajrzyj i napewno się tego nauczysz
i zrozumiesz
( zajrzyj i napewno się tego nauczysz
i zrozumiesz zad4/ zobacz pod hasłem: geometria analityczna − odległość punktu od prostej
tylko podstawić do wzoru i to wszystko:
Myślę,że dasz radę i sama się tego nauczysz, to nie jest trudne
zad4/ zobacz pod hasłem: geometria analityczna − odległość punktu od prostej
tylko podstawić do wzoru i to wszystko:
Myślę,że dasz radę i sama się tego nauczysz, to nie jest trudne podobnie zad; 5/
też pod hasłem geometria analityczna
−−−−− długość odcinka i współrzędne środka odcinka)
Wierzę ,że sobie poradzisz
podobnie zad; 5/
też pod hasłem geometria analityczna
−−−−− długość odcinka i współrzędne środka odcinka)
Wierzę ,że sobie poradzisz Powodzenia!.... jak coś , to pisz i podaj jakie masz rozwiązania!
Sprawdzimy i pomożemy na bank
Powodzenia!.... jak coś , to pisz i podaj jakie masz rozwiązania!
Sprawdzimy i pomożemy na bank Powodzenia!
Powodzenia!
 zad4/ musisz napisać równanie prostej w postaci ogólnej: AX +By +C=0
x − y +1=0 czyli A= 1 B= −1 C=1
P( −1, −2) czyli xo = −1 yo = −2
teraz do wzoru:
d=U{I 1*(−1) +(−1)*(−2) + 1 I}{√ (−1)2 + 12
zatem:
zad4/ musisz napisać równanie prostej w postaci ogólnej: AX +By +C=0
x − y +1=0 czyli A= 1 B= −1 C=1
P( −1, −2) czyli xo = −1 yo = −2
teraz do wzoru:
d=U{I 1*(−1) +(−1)*(−2) + 1 I}{√ (−1)2 + 12
zatem:
| I −1 +2 +1I | ||
d = | ||
| √2 |
| 2 | ||
d= | ||
| √2 |
| 2*√2 | ||
d= | ||
| 2 |


| I1*(−1) +(−1)*(−2) +1I | ||
d= | ||
| √(−1)2 + 12 |
 Podaj ... swój nr. ( choć rzadko przystaję na podawanie gg
zrobię dla Ciebie wyjątek
Podaj ... swój nr. ( choć rzadko przystaję na podawanie gg
zrobię dla Ciebie wyjątek