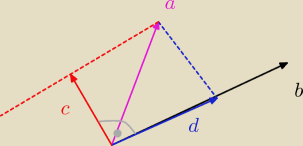
Składowe prostopadłe do b Nienor: a=[3,−2,4], b=[4,−3,−1]

	aob		12+6−4
projekcja a na b=		b=		[4,−3,−1]=
	|b|2		√16+9+1

	14		56		−42		−14
		[4,−3,−1]=[		,		,		]=d
	√26		√26		√26		√26

	56		−42		−14
c=a−d=[3,−2,4]−[		,		,		]
	√26		√26		√26

Artur_z_miasta_Neptuna: wygląda dobrze ... chociaż się nie zagłębiałem ale możesz sprawdzić robiąc tak: mając wektor b jesteś w stanie podać wektor o takiej samej długości, prostopadły do b i wtedy projekcja a na ten prostopadły i masz już wektor c

anwaro: u × ( v × w ) = ( u ⋅ w ) v − ( u ⋅ v ) w udowodnić z pomocą symbolu całkowicie antysymetrycznego