Stereometria: Przekroje wielościanów d4mian: 1) Suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 42, a pole jego powierzchni bocznej wynosi 72 cm². Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy oraz środek przeciwległej krawędzi bocznej i, jako przekrój, otrzymano trójkąt równoramienny. Oblicz cosinusy kątów tego trójkąta (rozpatrz dwie możliwości).

	41		3		17		2
Odp: cosα =		, cosβ =		lub cosα =		, cosβ =
	50		10		25		5

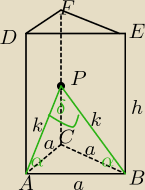
Mila: 6a+3h=42 /:3 suma krawędzi P_b=3a*h=72 /:3 2a+h=14 ⇔h=14−2a a*h=24 ⇔a*(14−2a)=24⇔a²−7a+12=0 Δ=1 a₁=3 lub a₂=4 h₁=14−2*3=8 lub h₂=14−2*4=6 I) a=3 i h=8 z tw. cosinusów k²=4²+3²⇔k=5 a²=k²+k²−2k²cosδ⇔3³=5²+5²−2*25cosδ 9=50−50cosδ⇔−41=−50cosδ

	41
cosδ=
	50

k²=a²+k²−2akcosα⇔0=3²−2*5*3cosα⇔−9=−30cosα

	9		3
cosα=		=
	30		10

II) a=4 i h =6 oblicz sam wg wzoru