zadania z geometrii analitycznej Sandra: bardzo proszę o pomoc w poniższych zadaniach. kompletnie nie mam zielonego pojęcia jak zabrać się za te zadania. 1) Punkt A(7,3) jest wierzchołkiem, zaś punkt S(3,2) środkiem symetrii kwadratu ABCD. Wyznacz pozostałe wierzchołki kwadratu ABCD i napisz równanie okręgu wpisanego w ten kwadrat. 2) Punkty A(−1,−6) i B(3,−3) są kolejnymi wierzchołkami rombu ABCD. Wierzchołek C należy do prostej o równaniu x+y=5. Znajdź współrzędne punktów C i D.

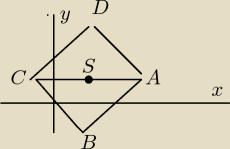
AS: Zad. 1 A(7,3) , S(3,2) S środek odcinka AC 1/2*(xA + xC) = xS ⇒1/2(7 + xC) = 3 ⇒ xC = −1 1/2*(yA + yC) = yS ⇒1/2(3 + yC) = 2 ⇒ yC = 1 ⇒ C(−1,1) Równanie prostej BD − prostopadłej do AC i przechodzącej przez S mAC = (yA − yC)/(xA − xC) = (3 − 1)/(7 − (−1)) = 2/8 = 1/4 mBD = −1/mAC = −4 y − yS = mBD*(x − xS) ⇒ y − 2 = −4*(x − 3) ⇒ y = −4*x + 14 Równanie okręgu opisanego na kwadracie R² = (xA − xS)² + (yA − yS)² = (7 − 3)² + (3 − 2) = 17 (x − xS)² + (y − yS)² = R² (x − 3)² + (y − 2)² = 17 równanie okręgu Rozwiązując układ równań (x − 3)² + (y − 2)² = 17 i y = −4*x + 14 otrzymamy współrzędne wierzchołków B i D Po uporządkowaniu x² − 6*x + 8 = 0 ⇒ x1 = 2 , x2 = 4 , y1 = 6 , y2 = −2 B(4,−2) , D(2,6) część druga − znalezienie równania okręgu wpisanego promień okręgu wpisanego r jest połową długości boku kwadratu AB: AB² = (xA − xB)² + (yA − yB)² = (7 − 4)² + (3 + 2)² = 9 + 25 = 34 AB = √34 r = 1/2*AB = 1/2*√34 równanie okręgu (x − xS)² + (y − yS)² = r² (x − 3)² + (y − 2)² = 34/4