nierówność trygonometryczna Oliwka552: sinxsin2x>0

krystek: sinx>0 i sin2x>0 lub sinx<0 i sin2x<0 lub graficznie na podstawie wykresów tych funkcji

kkk: ale jak narysować sin2x>0 ?

Basia: a może tak: sinx*sin2x > 0 sinx*2sinx*cosx > 0 2sin²x*cosx>0 ⇔ sinx≠0 ∧ cosx>0

Maslanek: A może inaczej: sin2x=2sinx*cosx Zatem sinx*sin2x=2sin²x*cosx 2sin²x*cosx>0 Więc cosx>0 oraz sin²x≠0. x∊(−π/2+2kπ,π/2+2kπ)\{2kπ}

kkk: a jeśli muszę to rozwiązać metodą graficzną?

ZKS: Można też tak

	1		1		x + 3x		3x − x
sin(x)sin(2x) =		* 2sin(x)sin(2x) =		* 2sin(		)sin(		) =
	2		2		2		2

1
	(cos(x) − cos(3x))
2

1
	(cos(x) − cos(3x)) > 0
2

cos(x) > cos(3x)

ZKS: Z tego chyba łatwo będziesz miał rozwiązać metodą graficzną i algebraiczną.

kkk: czyli jeśli chcę graficznie, to najpierw rysuję cosx potem cos3x i wtedy szukam przedziału dla kt. cosx>cos3x? tylko problem w tym, że nie wiem jak narysować cos3x..

ZKS: 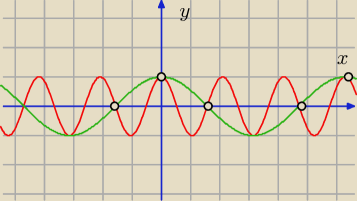y = cos(3x) y = cos(x)

kkk: Dziękuję

ZKS: Nie ma za co proszę bardzo.