wzajemne położenie prostej i okręgu Liliana: mam kilka zadan prosze o pomoc i w miare możliwości wytłumaczenie : 1. oblicz odległość punktu p od prostej l, jeśli p(1,3) l:y−3=0 2. określ wzajemne położenie prostej l i okręgu o , jeśli o: (x+5)²+y²=1 l:y=x−5 3. wyznacz współrzędne punktów współnych ( o ile istnieją ) prostej l i okręgu o(S,r). W każdym przypadku wykonaj rysunek .. 0:x²+y²=9 l:y=1/3x−1 4.napisz równanie stycznych do okręgu o i równoległych do prostej k o:(x−2)²+(y−1)²=4 k:y=2x 5.napisz równania stycznych do okręgu o i prostopadłych do prostej k o:(x+2)²+(y−3)²=1 k:y=x 6. napisz równanie stycznych do okręgu o i przechodzących przez punkt A , jeśli : o: x²+y²=4 a(6,−2) 7. zbadaj w zalęzności od wartości parametru m (m∊r) liczbe punktów współnych okręgu o z prostą l, jeśli : o: x²+y²=25 l:4x+3y=m

think: zadanie 1. wzór Ax + By + C = 0 oraz P = (a, b) d = U{|Aa + Bb + C|}{√A² + B² zadanie typu podstaw do wzoru...

Liliana: ok, ok. trzeba podstawić do wzoru. Mam raczej problem z zadaniami od 3 włącznie..

think: zadanie 2. możliwości dwie 1) narysować układ współrzędnych, zadaną prostą i zadany okrąg i z obrazka odpowiedzieć, czy są rozłączne, styczne, czy prosta przecina okrąg w dwóch punktach 2) można rozwiązać równanie kwadratowe (x + 5)² + (x − 5)² = 1 i w zależności od tego co wyjdzie Δ > 0⇒ dwa punkty wspólne; Δ = 0⇒ obiekty styczne; Δ < 0 ⇒obiekty rozłączne

think: Liliana to po co napisałaś te z którymi nie masz problemu

Liliana: chciaąłm sie upewnić, czy dobrze myśle...

think: 3 robisz analogicznie jak drugie, rozwiązujesz równanie kwadratowe x² + y² = 9

	1
y =		x − 1
	3

	1
x2 + (		x − 1)2 = 9
	2

chyba że nie miałaś jeszcze równań kwadratowych, to x² + y² = 9 ⇒ mamy do czynienia z okręgiem o środku w punkcie (0,0) i r = 3

	1
rysujesz to na układzie współrzędnych tam samo prostą y =		x − 1 i odczytujesz z
	3

wykresu...

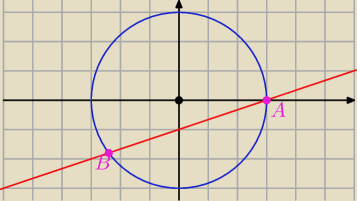
Aga1.: 3) Rysujesz okrąg o środku S(0,0) i promieniu r=3 i prostą Algebraicznie. Rozwiąż układ równań x²+y²=9 y=1/3x−1

think: 4. prosta równoległa do y = 2x to prosta postaci y = 2x + b ma być styczna do okręgu, zatem Δ = 0 (x − 2)² + (2x + b − 1)² = 4 i ponownie liczysz Δ i wyjdą Ci dwa rozwiązania..

Liliana: w 3 wystarczy rozwiazac ukłd rownan ?−

think: no spróbuj... Aga podała Ci rozwiązanie graficzne, teraz Ty rozwiąż układ równań i zobacz czy wyszło Ci to samo.

think: zad 5. robi się identycznie jak 4. tylko warunek na proste prostopadłe wygląda inaczej niż na równoległe. Prosta prostopadła do y = x ma postać y = −x + b a później znowu podstawić i liczyć jak 4.

Liliana: a mam takie pytanie, jeśli chodzi o Δ.... bo ta delta dotyczy czego, przy rownaniach kwadratowych Δ<o oznacza to że parabola nie ma miejsc zerowych ... tylk onie wiem jak te wiadomości przełożyć na koło . ... i w ogóle jak to porównać z tą prostą, z która koło lub okrąg ma mieć punkty współne...

think: hehehe, ano jak podstawić równanie prostej pod y w równaniu okręgu, to jak wyjdzie Ci Δ > 0 to oznacza że są dwa punkty wspólne okręgu i prostej, Δ = 0 to jest jeden punkt wspólny, Δ < 0 brak punktów wspólnych

Liliana: ok, a jesli chodzi o 6 ?

Liliana: 6 zadanie ..

aniabb: bo jak wstawisz równanie prostej do okręgu to wyjdzie Ci parabola czyli po prostu równanie kwadratowe

aniabb: jedna styczna x=−2

Liliana: czyli np. jak mam równanie okręgu o: 5x²−40x+82=0 i równanie prostej y=8−2x to po prostu wstawiam tak 5x²−40x+82=8−2x ? i wtedy licze Δ po przełożeniu wszystkiego na lewą strone?

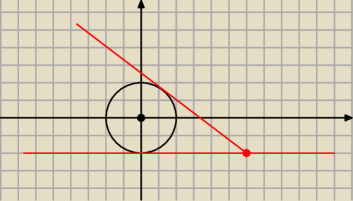
aniabb: poprawka .. pierwsza to y=−2

think: ajj zrobiłam mały błąd w zadaniu 3

	1		1
zamiast		wpisałam
	3		2

Liliana: aniabb prosze wytłumacz mi to, jestem kompletnie zielona jesli chodzi o zadanie 6:(:(

think: Liliana równanie okręgu np (x − a)² + (y + b)² = r² jak za y to za y nie za zero

aniabb: jak masz równanie okręgu y²+x² +...=0 to wstawiasz prostą y=ax+b w miejsce y (ax+b)²+x² +.... = 0 i deltę

Liliana: aha, ok. Tylko dalej nie wiem co z tym 6:(:(

aniabb: prosta styczna ma równanie y=ax−6a−2 wstawiasz do równania okręgu (ax−6a−2)² +x² =4 liczysz deltę i Δ=0 żeby była styczna

aniabb: dobrze zgadłam wyjdzie a=−3/4 czyli styczna ma równanie y= −3/4 x +10/4

Liliana: nie rozumiem tego

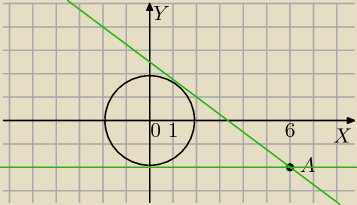
Mila: o: x²+y²=4 A(6,−2) s: y=ax+b⇔ ax−y+b=0 i A∊s a*6+2+b=0⇔b=−2−6a s: ax−y−2−6a=0 odległość od punktu (0;0) jest równa 2

|a*0 −0−2−6a|
	=2
√a2+1

|2+6a|=2√a²+1 Rozwiąż

think: zadanie 6 y = ax + b do tej prostej należy punkt (6, −2) −2 = 6a + b ⇒ b = −6a − 2 y = ax − 6a − 2 x² + y² = 4 x² + (ax − 6a − 2)² = 4 x² + a²x² − 12a²x − 4ax + 36a² + 24a + 4 = 4 x²(1 + a²) − x(12a² + 4a) + 36a² + 24a = 0 mają być styczne więc Δ = 0 Δ = (12a² + 4a)² − 4(1 + a²)(36a² + 24a) === 0

Liliana: dalej nie rozuymiem

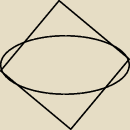
Maja: oblicz pole zacieniowanej figóry to figóre w środku boki mają po 8 bo to kwadratnestety ten rysunek nie jest idealny