Funkcja odwrotna mesia666: Wyznacz funkcję odwrotną do danej: f(x)=x²−1 dla x∊<0,∞) Czy, aby funkcja posiadała funkcję odwrotną to musi mieć dziedzinę R?

Artur_z_miasta_Neptuna: y=x²−1 wyznaczamy f⁻¹ x=y²−1 x+1 = y² y = √x+1 gdyby f(x) miała D_f = R to by nie istniała funkcja odwrotna odsyłam do warunków jakie musi spełnić funkcja, aby posiadała funkcję odwrotną

mesia666: na wykresie to wiem, że każdemu argumentowi musi być przyporządkowany jedna wartość ale jak to się liczy

mesia666: i jeszcze pytanie odnośnie pierwiastkowania nie powinno być y = √x + √1

Aga1.: Funkcja musi być różnowartościowa. Każda prosta równoległa do osi OX ma z wykresem funkcji różnowartościowej co najwyżej jeden punkt wspólny.

Aga1.: Nie , bo obliczasz pierwiastek z całej prawej strony, a nie z każdego składnika z osobna √a+b≠√a+√b.

mesia666: no dobra pierwiastki zrozumiałem, ale jak obliczyć różnowartościowość funkcji

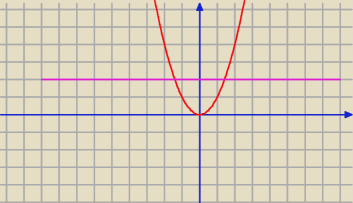
Aga1.: Np. Wiedzieć jak wygląda wykres lub narysować .Można dowodzić z definicji, ale w tych zadaniach chyba nie jest konieczne. Funkcja y=x² i każda funkcja kwadratowa w R nie jest różnowartościowa, bo istnieje prosta równoległa do osi x, która ma więcej niż jeden punkt wspólny z wykresem.

mesia666: Aha z tego to chyba zrozumiem to, bo widziałem obliczenia tego typu (tylko inny przykład) f(x) = 3^x f(x₁) = 3^x1 f(x₂) = 3^x2 3^x1 = 3^x2 i to wszystko i tego nie rozumiem

Artur_z_miasta_Neptuna: bo tak się de facto sprawdza różnowartościowość funkcji

Aga1.: Napisz definicję funkcji różnowartościowej

mesia666: Funkcja różnowartościowa jest wtedy, gdy dowolnemu argumentowi odpowiada tylko jedna wartość

Aga1.: f(x₁)=f(x₂)⇒x₁=x₂ 3^x₁=3^x₂⇒x₁=x₂ (własność funkcji wykładniczej)

Artur_z_miasta_Neptuna: czyli funkcja jest różnowartościowa gdy dla dowolnych x₁,x₂ takich, że: x₁≠x₂ wynika że f(x₁) ≠ f(x₂)

mesia666: czyli można sobie podstawić za x₁ i x₂ różne liczby i na liczbach to obliczyć

Aga1.: Nie , tylko na literkach. (już Ci napisałam szkic ) Tylko sprawdź, jaką masz podaną definicję. Z tego co zapisałaś wnioskuję, że trochę inaczej zapisaną niż napisał Artur.

mesia666: ja ogólnie definicji nie mam tylko wnioskuje po przykładach

Aga1.: I chyba o to chodzi.

mariuszek: zeby wyznaczyc funkcje odwrotna musisz wyliczyc x przeciez a nie y. Moj wynik to x = √y+1

Aga1.: Zmieniasz nazwę zmiennych na początku lub na końcu. Twój wynik jest poprawny x=√y+1 i dalej y=√x+1

mariuszek: skoro juz taka latwo idzie wyznaczanie funkcji odwrotnych to mam kilka przzykladow: y=3+log₅(x+3) nie mam pojecia jak sie za to zabrać

Aga1.: Od razu zamieniam zmienne (można na końcu) log₅(y+3)=x−3 5^x−3=y+3 y=5^x−3−3.