Liczby zespolone, help magda: ZnaleŜć postacie trygonometryczne liczb zespolonych z₁ = 2√3 − 2i oraz z₂ = −1 + √3i a następnie obliczyć z₁³ * z₂² nie wychodzi

aniabb: cóż Ci nie wychodzi

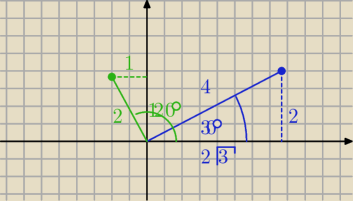
aniabb: z1 = 4(cosπ/6 +i sinπ/6) z2= 2(cos4π/6 +i sin4π/6)

magda: obliczylam postacie trygonometryczne ktora wynosza z₁=4(cos^11π₆ + isin^11π₆) i z₂=2(cos^2π₃+isin^2π₃) a nastepnie wymnozylam te liczby korzystajac z Moivre'a

magda: czemu tak? w z₁ sin jest ujemny wiec to chyba bedzie 4 cwiartka?

aniabb: no tak..zrobiłam 2√3 + 2i to jeszcze raz

aniabb: a no to masz dobrze nie muszę rysować

magda: i jak dalej? powinno wyjsc 128(−√3 + i)

aniabb: no to teraz do potęgi z1³ = 4³ (cos(3*11π/6) + i sin(3*11π/6)) = 64*(0+i*(−1)) = −64i

aniabb: z2 ² =2²(cos(2*2π/3 +i sin(2*2π/3)) = 4(−1/2 +i (−√3/2) = −2−2√3

aniabb: no i mnożymy −64i*( −2−2√3 i ) = 128i −128√3

magda: czemu sin^π₂ = −1 ?

aniabb: sin 11π/2 = −1

magda: aa ok, zagalopowalam sie dzieki!

magda: a cos takiego z₁² / z₂⁵ ?

aniabb: z1² = 4² (cos(2*11π/6) + i sin(2*11π/6)) = 16(1/2 +i (−√3/2) = 8−8√3 i z2⁵ = 2⁵(cos(5*2π/3 +i sin(5*2π/3)) = 32(−1/2 +i (−√3/2) = −16−16√3 i więc

8−8√3 i		1−√3 i		(1−√3 i)(1−√3 i)
	= −1/2		= −1/2
−16−16√3 i		1+√3 i		(1+√3 i)(1−√3 i)

	1−2√3 i −3
−1/2		=−1/8 (−2−2√3 i) = 1/4(1+√3 i )
	1+3