Problem z liczbą zespoloną. sprd.: Witam! Mam problem z liczbą zespoloną: ³√(−1+i)=

	3
Muszę zamienić to na postać trygo i cały czas wychodzi mi, że będzie to √2(cos		π +
	4

	3
isin		π) a odpowiedzi są inne.
	4

Co robię źle? pozdrawiam

sprd.: hmm?

sprd.: ogarnia ktoś zespolone czy nikt?

Basia: |−1 + i| = √(−1)²+1² = √2

	−1		√2
cosα =		= −
	√2		2

	1		√2
sinα =		=
	√2		2

	3π
α=
	4

−1+i = √2*(cos^3π₄ + i*sin^3π₄) i teraz z wzorów Moivre'a

	3π4+2kπ		3π4+2kπ
3√−1+i = 3√√2(cos		+i*sin		) =
	3		3

	3π+8kπ		3π+8kπ
6√2(cos		+i*sin		)
	12		12

k=0

	π		π
3√−1+i = 6√2(cos		+i*sin		) =
	4		4

	√2		√2
6√2*(		+i*		) =
	2		2

21/6*21/2
	(1+i) =
2

24/6		22/3		3√4		3√4
	(1+i) =		(1+i) =		+ i*
2		2		2		2

podstawiaj dalej k=1, k=2 itd. aż Ci się wyniki nie zaczną powtarzać

Basia: jak będziesz miał wątpliwości to będę za jakieś półtorej godziny idę kupić mysz moja właśnie zdechła i wszystko robię strasznie wolno

sprd.: aaaa ale postać trygo wyszła mi dobrze, czyli kąt jest 3/4π. Dziękuje

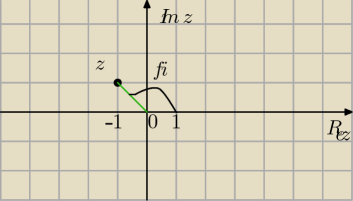
Mila: z=−1+i na płaszczyźnie zespolonej to punkt (−1;1) |z|=√2

	3π
φ=		odczytujesz argument z rysunku.
	4