dowód
Madzia: Udowodnić, ze jeśli przekątne w czworokącie ABCD przecinają się pod katem prostym, to
|AB|2+|CD|2=|AD|2+|BC|2
13 lis 11:05
Artur_z_miasta_Neptuna: 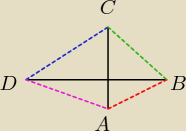
|AB|
2 = d
12 + e
22
|BC|
2 = d
22 + e
22
|CD|
2 = d
22 + e
12
|AD|
2 = d
12 + e
12
gdzie d
1,d
2 ... rozkład pionowej przekątnej
e
1,e
2 ... rozkład poziomej przekątnej
zsumuj tak jak masz w zadaniu ... to wyjdzie równość
13 lis 11:10
Madzia: proszę, powiedz mi czym jest ten rozkład pionowej i poziomej przekatnej?
13 lis 12:12
krystek: Artur miał na myśli , wyznaczenie boków przy pomocy części przekatnych e=e1+e2(co autor
miał na myśli− interpretuję)
13 lis 12:18
aniabb: czarna linia od środka do C to d2
czarna linia od środka do A to d1
czarna linia od środka do B to e2
czarna linia od środka do D to e1
13 lis 12:20
Artur_z_miasta_Neptuna: rysunek był za mały aby 'wciskać' te d1,d2,e1,e2 ... liczyłem na to że Madziu się domyślisz
z opisu o co mi chodziło
13 lis 12:24
Madzia: dzieki bardzo. Wcześniej też tak własnie rozpisałam to zadanie, ale myślalam, ze to nie bedzie
dobrze.

13 lis 12:51
 |AB|2 = d12 + e22
|BC|2 = d22 + e22
|CD|2 = d22 + e12
|AD|2 = d12 + e12
gdzie d1,d2 ... rozkład pionowej przekątnej
e1,e2 ... rozkład poziomej przekątnej
zsumuj tak jak masz w zadaniu ... to wyjdzie równość
|AB|2 = d12 + e22
|BC|2 = d22 + e22
|CD|2 = d22 + e12
|AD|2 = d12 + e12
gdzie d1,d2 ... rozkład pionowej przekątnej
e1,e2 ... rozkład poziomej przekątnej
zsumuj tak jak masz w zadaniu ... to wyjdzie równość
