Sprawdzenie logarytmicznej nierownosci niecik: Mam prośbe odnośnie nierównosci logarytmicznej czy moze ktoś mi to sprawdzić i znaleźć ukryty błąd przez który nie mogę otrzymac dobrej odpowiedzi log₂(x−2)+log o podstawie ¹₂ (2x−3)>1 log₂(x−2)−log₂(2x−3)>1 log₂ ^x−2_2x−3>1 ^x−2_2x−3>2 4x−6>x−2 x>⁴₃ D 2x−3>0 x>³₂ wychodzi mi że x∊( ⁴₃, +∞) ALE w odpowiedziach pisze że ma wyjśc "nie ma rozwiazan Gdzie jest błąd

Ajtek: A dziedzinę ustaliłeś

Ajtek: I skąd się wzięło 4x−6>x−2?

niecik: x>³₂ tyle mi dziedzina wyszła a tamto mi sie wzieło przez wymnożenie

Ajtek: A jak wymnożyłeś to raz? Dwa, a sprawdzenie warunku x−2>0 nie jest potrzebne z pierwszego logarytmu?

niecik: wymnożyłem to na krzyż ^x−2_2x−3>²₁

Beti: 1) źle wyznaczyłeś dziedzinę, bo powinny być 2 warunki: x−2>0 i 2x−3>0, co daje: x>2 2) źle rozwiązujesz nierówność wymierną −−> zamiast mnożyć przez mianownik trzeba np przenieść 2 na lewą stronę, sprowadzić do wspólnego mianownika i odjąć oba wyrażenia

niecik: właśnie nie wiem czy to na tym etapie sprawdza sie ta dziedzinę

Ajtek: Masz nierówność. Nie możesz tak zrobić, ponieważ nie wiesz jaki jest znak mianownika Przewal 2 na lewą stronę nierówności, później wspólny mianownik, a następnie mnożysz przez kwadrat mianownika.

Ajtek: Dziedzinę zawsze na początku ustalasz.

niecik: czyli według twoich wskazówek wychodzi x< ⁴₃ a D x>2

niecik: aj momencik bez kwadratu pomnozyłem

Ajtek: Wg kogo wskazówek?

Beti: po przekształceniu tej nierówności do postaci iloczynowej masz: (2x−3)(4−3x)> 0 co jest rozw. tej nierówności i co z tego rozwiązania spełnia warunek z dziedziny?

niecik: Δ<0 czyli brak rozwiazan i zgadza sie to z odpowiedzią ?

Ajtek: Jeżeli szukałeś Δ to odpowiedz jak ma ta parabolka ramiona skierowane, w górę/dól?

niecik: 6x²−15x+12<0 2x²−5c+4<0 Δ=25−32 Δ<0 tak mi wyszło

Ajtek: A skąd 6x²

niecik: raczej w górę

Ajtek: Zerknij na post Beti z godz 22:51 i odpowiedz na pytanie skąd 6x² Beti dzięki za pomoc .

niecik: pomyliłem się w obliczeniach nie to policzyłem

niecik: jak sie nie pomyliłem to powinno wyjsc tyle x<− u{5]{3}

niecik: x< −5/3

Ajtek: A odpowiedź na pytanie jak z ramionami parabolki?

niecik: to już robi sie smieszne znowu sie machnąłem

niecik: (−3x−5)(2x−3)>0 tak ma być po przeniesieniu dwójki na lewą stronę ?

Ajtek: Wiesz co nie liczę. Ja tylko podpowiadam .

niecik: czy tak (−3x+1)(2x−3) >0

niecik: tak ma być już raczej napewno (4−3x)(2x−3) >0

niecik: i z tego 8x−12−6x²+9>0

niecik: −6x²+8x−3>0

niecik: 6x²−8x+3<0

niecik: Δ=64−72 Δ<0

Beti: niecik nie wymnażaj, tylko z każdego nawiasu wyznacz miejsce zerowe przyrównując wyrażenie z nawiasu do zera

niecik: czyli z tego wychodzi że funkcja nie ma miejsc zerowych i rośnie w przedziale R₊ ?

niecik: czyli te miejsca x₁= ⁴₃ v x₂= u{3}{2] ?

Beti: bingo

niecik: ok majac te miejsca co teraz ?

Beti: naszkicuj parabolkę i odczytaj rozwiązanie nierówności

Ajtek: A jak ramiona paraboli? Góra/dół?

niecik: nawet tam gdzie wymnażałem ta funkcję powinno być 8x−12−6x²+"9x">0

niecik: (4−3x)(2x−3) >0 ale ramiona z tej nierówniości

Ajtek: F. kwadratowa: ax²+bx+c Jeżeli a>0 to parabolka jest uśmiechnięta, ramiona w górę Jeżeli a<0 to parabolka smutna, ramiona w dół.

niecik: wychodzi że a<0

Piotr: no tak

niecik: x∊(⁴₃, ³₂ ) tyle wychodzi przedział

Piotr: i nalezy do dziedziny ?

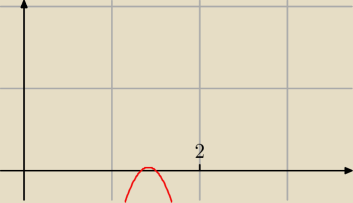
Ajtek: Zatem ramiona w dół. Nasza dziedzoina to x>2 A z paraboli wychodzi tak jak na rysunku. Część wspólna jest zbiorem pustym.

Beti: i teraz część wspólna z dziedziną

niecik: Dziekuję wam wszystkim że wytrwaliście ze mną tyle czasu i mieliście na tyle cierpliwosci goraco pozdrawiam was wszystkich Sam sobie napewno bym z tym nie poradził ale dzieki wam stało się to mozliwe dziekuje bardzo jeszcze raz gorąco pozdrawiam wszystkich

Ajtek: Nie ma sprawy. Zacznij myśleć i stosować matematukę do liczenia, będzie łatwiej .

Beti:

niecik: jesteście wielcy pomodle się za was obiecuje

Ajtek: Ja również dziękuję Beti, Piotr .

Piotr: mój wkład byl prawie żaden

Ajtek: Ale jednak znaczący .

niecik: każdy wklad się liczy dzięki dobrej nocy wam życze

Beti: do usług