zespolone asdasdas: Podać interpretację geometryczną zbioru liczb zespolonych spełniających warunek: arg(z+1)=π

asdasdas:

asdasdas:

asdasdas:

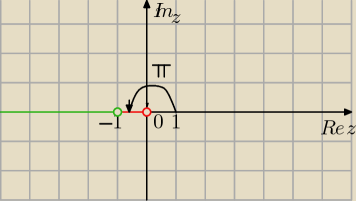
Mila: na czerwono liczby z o argumencie głównym φ=π (ujemna półoś OX bez (0;0) z+1 o argumencie równym π to zbiór X<−1 i y=0 ( zielony zbiór) Obliczenia: z = x+iy z+1 = (x+1)+iy |z+1|=√x+1)²+y² z+1=|z+1|(cosφ+isinφ)

	x+1
cosφ=		⇔cosπ=−1
	√x+1)2+y2

x+1
	=−1⇔(x+1)=−√x+1)2+y2 ma sens dla x+1<0⇔x<−1
√x+1)2+y2

(x+1)²=(x+1)²+y² y=0 i x<−1 spr. dla x=−1; z=−1+i*0; z+1=0+i*0 punkt (0,0) arg(z+1)≠π