moduł
trw: Rozwiąż równanie:
|x| − |x+1| =2
12 lis 22:14
Beti:
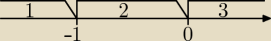
Rozpatrz to równanie w tych trzech przedziałach
12 lis 22:23
dumka: |x| − |x+1| = 2
przedziały:
(−
∞;−1> , (−1, 0> , (0,+
∞)
1. dla x ∊ (−
∞, −1)
|x| < 0 −x
|x+1| ≤ 0 −x−1
Podstawiamy
−x − (−x−1) =2
−x + x+1 = 2
0 = 1 czyli ten przedział (−
∞; −1) bierzemy pod uwagę
2. dla x ∊ (−1;0>
|x| ≤ 0 −x
|x+1| > 0 x+1
Podstawiamy
−x −x+1 = 2
−2x = 1/ : (−2)
| | 1 | | 1 | |
x = − |
| czyli ten przedział (−1;0>, bo − |
| należy do tego przedziału |
| | 2 | | 2 | |
3. dla x ∊ (0; +
∞)
|x| > 0 x
|x+1| > 0 x+1
Podstawiamy czyli ten przedział bierzemy pod uwagę
x − x−1 = 2
o = 3
czyli moim zdaniem rozwiązaniem są wszystkie liczby rzeczywiste, ale mogę się mylić
12 lis 22:44
Beti: Trochę namieszane, bo:
1) rozpatrywane przedziały to: (−∞,−1); <−1,0); <0,+∞)
2) rozwiązania:
pkt 1. dobrze rozwiązane równanie, ale wniosek jest taki, że otrzymujesz sprzeczność, czyli w
tym przedziale równanie nie ma rozwiązania
pkt 2. złe równanie. Powinno być tak:
−x − (x+1) = 2
−x − x − 1 = 2
−2x = 3
ale ta liczba nie należy do przedziału <−1,0), więc również w tym przedziale równanie nie ma
rozwiązania
pkt 3. dobre równanie i dobrze rozwiązane. Znowu jest sprzecznośc, więc równanie nie ma tu
rozwiązania
Sumując wnioski z punktów 1. − 3. widzimy, że to
równanie nie ma wcale rozwiązań.
12 lis 23:02
dumka: no tak masz racje pomyliłam się ale też tak myślałam, że mi te −1/2 nie pasuje, bo nawet jak
podstawiłam to mi nie pasuje. Dzięki
12 lis 23:08
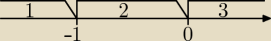 Rozpatrz to równanie w tych trzech przedziałach
Rozpatrz to równanie w tych trzech przedziałach