PW: Oznaczmy symbolem r różnicę ciągu arytmetycznego. Boki trójkąta mają długości a, a+r, a+2r.
Wiadomo, że promień R okręgu wpisanego poprowadzony do punktu styczności z bokiem trójkąta
jest prostopadły do tego boku, a więc pole P trójkąta można obliczyć jako sumę trzech
trójkątów o wysokościach R:
2P = aR + (a+r)R + (a+2r)R
(liczę podwojone pola, żeby nie pisać ułamków). Rysunek zrobisz samodzielnie.
2P = 3aR + 3rR
2P = 3(a+r)R.
Jeżeli symbolem h oznaczymy wysokość trójkąta opuszczoną na bok o długości (a+r), to
2P = (a+r)h,
a więc
(a+r)h = 3(a+r)R,
h = 3R
co należało udowodnić.
No i okazałem się o 8 minut gorszy niż Bogdan. Pora spać.

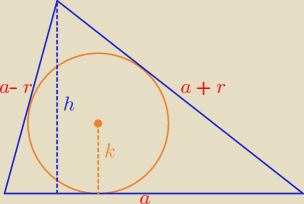 Ciąg arytmetyczny (an): a1 = a−r, a2 = a, a3 = a+r.
Ciąg arytmetyczny (an): a1 = a−r, a2 = a, a3 = a+r.
