pytanie tn: Logarytmy, dziwna, bardzo dziwna rzecz: logx² = 2log x I teraz dziedzina tego pierwszego to x∊R − {0} zaś drugiego x > 0 co jest grane?

Piotr:

	x2
y =		D = R\{0}
	x

y = x D=R dziwne

Mila: logx²=2log|x|

tn: nom, co tu jest grane?

tn: aha, w ten sposób. Ale skąd taka pewność? We wzorach tego nie ma przecież, tego modułu.

Mila: Wzór podany przez Ciebie 21:16 jest słuszny dla x>0. Jeśli chcesz narysować wykres logx², to rysujesz y=2 logx dla x>0 i odbijasz symetrycznie względem OY.

tn: nie wiedziałem Dzięki mila A można to jakoś fajnie uzasadnić? Może wprost z def?

tn: Czyli jakby tą dziedzinę ciągniemy dalej, mimo przekształceń? Kto by pomyślał,a przykład Piotra?

Nienor: logarytmu Nie bardzo. To wynika z tego, że √x²=|x|, anie x. A co z przykładem Piotra

Mila: Dziedzinę piszesz ( u Piotra) dla początkowej funkcji, a potem przekształcasz. W przykładzie log x obowiązuje −" liczba logarytmowana dodatnia".

Piotr: dziedzine wyznacza sie dla pierwotnej funkcji, wielomianu

Piotr: wyrażenie wymierne mialo byc

Mila:

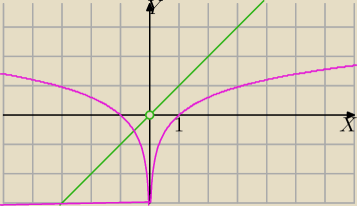
	x2
1) f(x)=		=x i x≠0 po przekształceniu, pamiętamy o dziedzinie.(zielony)
	x

Dla funkcji f(x) w innej postaci dalej obowiązuje w tym zagadnieniu D=R\{0} 2)y= logx² (różowy) w drugim układzie narysuję po przekształceniu

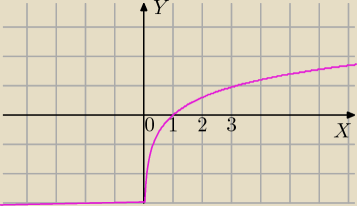
Mila: y=2logx ma sens dla x>0 D: x>0 Widzisz, że ten wykres różni się od wykresu funkcji y=logx²

tn: Na dobrą sprawę dziedzina y=logx to x> 0, ale już y=2logx to R−{0} Dziwne to: Skąd się formalnie bierze: logx² = 2log|x| tzn, ten moduł?

PW: Nic dziwnego tu nie ma. To szkolna sztampa: przed rozwiązaniem równania (czy też dowodem tożsamości) najpierw ustalamy dziedzinę (wspólną dla obu stron, bo o czym mówić, jeśli jedna ze stron równości nie ma sensu?). Dlatego wzór ma sens tylko dla x>0, i to na pewno jest w założeniach twierdzenia, gdyby tak do książki zajrzał ...

krystek: Ale mamy na początku: logx² czyli x²>0 ⇔x≠0

krystek: Inny zapis D=R/{0}