Trygonometria Kaliim: Pomóżcie zd z tryg!

	2		3		5
Wiedząc, że tgα=		, α∊(π;		π) Oblicz Sin(2α+		π)
	3		2		r

Kaliim:

	5
Poprawka tam pisze SIn(2α+		π) taki mały błędzik .
	4

Pomóżcie

Nienor:

	5π
x=
	4

	π		√2
sin(2α+x)=sin2αcosx+cos2αsinx=sin2αcos(π+		)+cos(π+{π}{4})sinx=−		(sin2α+cos2α),
	4		2

Dalej: sin2α=2sinαcosα cos2α=cos²α−sin²α I z danych:

	sinα		2
tgα=		=
	cosα		3

oraz sin²α+cos²α=1, czyli mamy dwa układy równań, z których wyliczymy sinα i cosα, dalej już pójdzie. Musisz tylko pamiętać, że w III ćwiartce sinus i kosinus są ujemne.

Kaliim: a mógłbyś mi napisać jeszcze wynik?

Kaliim: no ja to trochę innym sposobem liczyłem i tez mi wyszło,

	2√13		3√13
że sinus to −		i cos −
	13		13

Kaliim:

	√2
i potem wystarczy podstawić to pod −		(2sinαcosα+cos2 α−sin2 α)?
	2

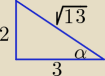
Nienor: Tak. Podstawić. A czy ten sposób nie polegał na narysowaniu trójkąta prostego przypadkiem, zaznaczeniu przyprostokątnych, obliczeniu przeciwprostokątnej i liczeniu z tego funkcji trygonometrycznych Jeśli tak to w zadaniu maturalnym, otwartym on nie przejdzie.

Kaliim: tak dokładnie na tym on polegał, dzięki za pomoc

Bogdan:

	√2		√2
... = −		(sin2α + cos2α) = −		(2sinα cosα + cos2α − sin2α) =
	2		2

	√2		√2
= −		(sin2α+2sinα cosα+cos2α − 2sin2α) = −		(sinα + cosα)2 + √2sin2α
	2		2

Bogdan:

	2		3		2		4
tgα =		i α∊(π,		π) ⇒ sinα = −		⇒ sin2α =
	3		2		√3		13

Nienor:

	−2√13
sinα=		, z twojego rysunku, ale jak już pisałam, to nie jest właściwa metoda na to
	13

dla kątów większych niż 90^o