wykres Magda: naszkicowac wykres arcsin(sinx) arcsinx potrafie narysowac, ale ten wykres to juz wyzsza matematyka tylko tyle wiem ze okres bedzie wynosic 2π...

Magda: podbijam

PW: f⁻¹(f(x)), to tak jak √x² (oczywiście trzeba uwzględnić przedziały, na których funkcja jest różnowartościowa, bo tam istnieje funkcja odwrotna).

Mila: D: x∊R

	π		3π
Funkcja jest okresowa i rozważę w przedziale <−		;		>
	2		2

	π
Dla x∊(U{−π}{2;		) dziedziną arcusa jest zbiór wartosci sinx czyli <−1;1>
	2

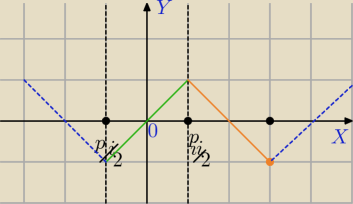
arcsin(sinx)=x zielona gałązka

	π		3π
dla x∊<		;		) sinus jest ujemny,
	2		2

	−π		π
argument x=π+v, gdzie v∊		;		)
	2		2

arcsin(sinx)=arcsin(sin(π+v))=arcsin(−sinv)=−arcsin(sinv)=−v=π−x

Magda: dziekuje a jak bedzie wygladal wykres sin(arcsinx)

aniabb: http://www.wolframalpha.com/input/?i=plot+sin%28arcsinx%29 ograniczony jak widać od <−1;1>

Magda: dzieki!

Mila: Wykres f(x)=sin(arcsinx)=x ma taką postać( jak wskazała Ania), ponieważ dziedziną f(x) jest przedział<1;1>.