Zbadaj przebieg zmienności funkcji kylo1303: Mam sobie funkcję f(x)= |x| * e^−x2 No i pojawily sie male problemy ... Najpierw licze sobie asymptoty: 1. pionowej nie ma 2. wyszlo mi ze jest pozioma y=0 , tyle ze dla isteniej punkt (0,0) (no i wez tu badz madry dlaczego tak jest) Ale ogolnie moje watpliwosci sprawdzaja sie do (|x|)' . Bo nie wiem czy moge sobie przyjac ze to jest =1, albo przynajmniej ze jest to ograniczone i "olać" w dalszych obliczeniach. f'(x)= (|x|)' * e^−x2 + |x| * (−2x)*e^−x2= e^−x2 * ((|x|)' − 2x * |x|) i co z tym dalej robic, bo mam przyrownac do 0 i sprawdzic >, < od 0 (wydaje mi sie ze (|x|)'=1 ale nie chce przez moje bledne zalozenie miec dalej zle obliczenia)

Basia: a jakie są lim_x→−∞ f(x) i lim_x→+∞ f(x)

Krzysiek: rozbij na przypadki x>0 wtedy: |x|=x ,(x)'=1 x<0 |x|=−x , (−x)' =−1 i x=0

Basia: ad.pochodna |x| nie możesz bo to nieprawda −1 dla x<0 |x|' = nie istnieje dla x=0 1 dla x>0

kylo1303: No o rozbiciu myslalem, ale uznalem ze musi dac sie inaczej. Tylko ze mam rozbic przy kazdej pochodnej? Bo to znacznie wydluzy zadanie (ktore i tak jakies krotkie nie jest) lim_x→∞ f(x)= 0 lim_x→−∞ f(x)= 0 (tutaj nie liczylem, wnioskuje po +∞)

kylo1303: No dobra, przykladowo licze pierwsza pochodna i rozbijam na przypadki:

	√2
x>0 : f'(x)=e−x2*(1−2x2) → f'(x)=0 → x=
	2

	√2
x<0 : f'(x)=e−x2*(−1+2x2) → f'(x)=0 → x=−
	2

No i to mam traktowac jako dwa rozne punkty stacjonarne i sprawdzac w kazdym przypadku co bedzie dalej, tj. f'(x) > /< 0 . Tyle ze wtedy to rozbije niejako na dwie funkcje ⇒ 2 razy wiecej roboty

Krzysiek: cóż zrobić, z reguły jak jest moduł to trzeba się bawić w przypadki... Można zauważyć, że funkcja jest parzysta i badać co się dzieje dla x>0 , wtedy dla x<0 będzie podobnie.

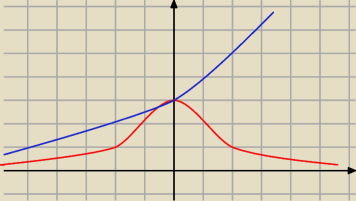
Basia: ad.17:13 to musisz policzyć bo jeżeli tę przy x→ −∞ policzyłeś dobrze to może oś OX będzie asymptotą poziomą ale tylko lewostronną, a może i nie może być takie coś jak narysowałam (dwie możliwości) nie liczyłam to tylko możliwości

kylo1303: no to ze jest parzysta to wiem Sprobuje zrobic po swojemu, moze ktos sprawdzi pozniej

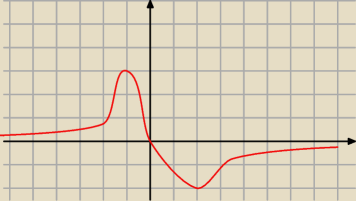
Basia: a nie soory, to nie jest dobry przykład może być takie coś

kylo1303: Basia Granice doprowadzilem do postaci:

	((|x|)')'−2
= lim		Jako ze licznik jest ograniczony to z tej postaci uznalem ze
	ex2*2x

leci do 0. jesli x→−∞ to w mianowniku bedzie −∞ * ∞, ale wydaje mi sie ze niczego to nie zmienia jesli chodzi o wynik.

kylo1303: Tzn, funkcja jest parzysta, wiec to tez mowi ze granice w +/− ∞ beda takie same

Basia: przecież w mianowniku masz nadal (+∞)*0 to skąd wiesz co to jest ?

Basia: policzę Ci te granice za chwilę

kylo1303: A skad 0? Chyba ze tobie chodizlo o granic lim_x→0 ale raczej nie o to.

Basia: oj bzdurę napisałam; dobrze masz f(x) = |x|e^−x2

	−x
limx→ −∞ f(x) = limx→ −∞ −x*e−x2 = limx→ −∞		=
	ex2

	−1		−1
limx→ −∞		=		= 0
	2x*ex2		−∞*(+∞)

	x
limx→ +∞ f(x) = limx→ +∞ x*e−x2 = limx→ +∞		=
	ex2

	1		1
limx→ +∞		=		= 0
	2x*ex2		+∞*(+∞)

no to może być takie cudactwo jak to co narysowałam o 17:27

Basia: i będzie bo ta Twoja funkcja to tak naprawdę −x*e^−x2 dla x<0 f(x) = x*e^−x2 dla x≥0 i tak ją dalej badaj

kylo1303: Dobra, w sumie to skonczylem, zaraz napisze najwazeniejsze pkt i narysuje w miare moich skromnych mozliwosci wykres, moze ktos zerknie i sprawdzi (albo zobacze co na to wolfram)

kylo1303: granice w +/− ∞ to 0, maxima lokalne wyszly mi dobrze. Wolfram nie pokazuje punktu przegiecia, ale mysle ze tez bedzie okej. Tak mniej wiecej wyszedl mi wykres.

	√2
a=
	2

	√6
b=
	2

czerwony to pkt. przegiecia a niebieski to max. Wartosci zaokraglilem. "coś poszlo nie tak, zacznij rysowac od nowa" ...

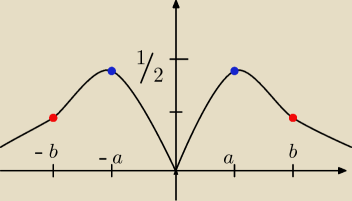
kylo1303: rysunek, proba 2

kylo1303: A tak jeszcze jakby ktos mi napisal co bedzie z asymptota pozioma, czy asymptota bedzie y=0 z wyjatkiem x=0 ?