prostokąt ABCD - analityczna geometria schatz: Prostokąt ABCD jest wpisany w okrąg x²+y²+4x+6y−12=0. Bok AB jest zawarty w prostej 2x+y−3=0. Znajdź: a) współrzędne wierzchołków prostokąta; b) pole prostokąta. mogłabym dostać w punktach co muszę robić pokolei, aby rozwiązać to zadanie?

Edek: a) oblicz punkty przecięcia prostej z okręgiem ( punkty A i B ) później poprowadź proste prostopadłej do tej prostej i przechodzące przez punkty A i B ( będą 2 różne proste ) i sprawdź gdzie się przetną z okręgiem b) z tym sobie już chyba dasz rade

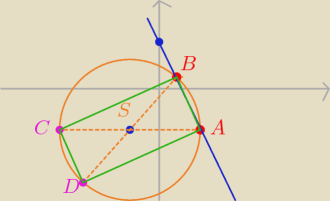
Eta: okrąg ma równanie: x² + y² +4x +6y − 12=0 więc ( x +2)² + ( y +3)²= 25 to S( −2, −3) r= 5 rozwiązując układ równań: ( x +2)² + ( y +3)² = 25 i y = −2x +3 otrzymasz współrzędne punktów A i B x² +4x + 4 +( −2x +6)² = 25 => x² +4x +4 +4x² − 24x + 36 − 25 =0 to: 5x² − 20x +15=0 /:5 x² − 4x +3=0 Δ= 4 √Δ=2 x₁ = 3 x₂= 1 to y₁ = −2*3 +3 i y₂ = (−2)*1+3 to: y₁ = −3 y₂ = 1 więc A( 3, −3) B( 1,1) ponieważ punkt S jest środkiem przekątnych więc możemy wyliczyć współrzędne punktu C ze wzoru:

	xA+ xC
xS =
	2

	yA +yC
yS=
	2

więc x_C = 2*x_S − x_A i y_C= 2*y_S − y_A zatem: x_C= 2*(−2) − 3 i y_C= 2*(−3) − (−3) to: x_C = −7 i y_C= −3 więc C( −7, −3) porównując współrzędne wektorów równych ( bo to prostokąt ) więc: → → DC= AB → → DC= [ x_C − x_D, y_C − y_D] i AB= [ x_B − x_A, y_B − y_A] mamy: −7 − x_D = 1 −3 i −3 − y_D = 1 +3 więc: x_D= −5 i y_D = −7 więc D( −5, −7) pole prostokąta już łatwo policzysz P= IABI * IADI policz IABI i IADI ....... ze wzoru na długość odcinka

schatz: dziękuję.

Eta: Oooo .... ucięło mi dokończenie zadania nie wiem czemu? dokańczam: porównując współrzędne wektorów równych: → → AB = DC otrzymasz współrzędne punktu D → → AB =[ x_B − x_A , y_B − y_A] i DC= [ x_C − x_D, y_C − y_D] więc: AB =[ 1 −3 , 1 +3] = [−2,4] i DC=[ −7 − x_D , −3 −y_D] zatem: −7 −x_D= −2 i −3 −y_D= 4 x_D= −5 i y_D= −7 to D(−5, −7) pole już prosto: P= IABI* IADI ...... policz długości boków ze wzoru na długość odcinka i podstaw do wzoru na pole

Eta: Oooo..... a myślałam ,że mi ucięło dokończenie zadania

Mariusz: Eta a możesz zajżeć do mojego postuProsze

wojciech:

joł: t

lol: dzieeeeki <3

lol: ααγβ to moje ulubine literki . SWAG