Kula. Cosinus. V.Abel: Kula wpisana w stożek ma pole powierzchni dwa razy mniejsze od pola powierzchni całkowitej stożka. Oblicz cos kąta nachylenia tworzącej do jego podstawy. Wyszedł mi cos= l / r gdzie r to promień podstawy. W odp jest jest 1/3 jak to zrobić?

V.Abel:

	r2
no i ten cos mi wyszedł		gdzie R to promień kuli
	8R2−r2

V.Abel: Proszę, help me ! ! !

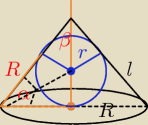
Mila: P_k=4πr² P_cs=πR²+πRl

	1
4πr2=		(πR2+πRl)⇔8πr2=πR2+πRl⇔
	2

8r²=R²+Rl /:R²

	r		l
8(		)2=1+
	R		R

	R
cosα=
	l

	α		1		α   sin2   2		cosα+1
tg2		=1+		⇔		=
	2		cosα		α   cos   2		cosα

Korzystam z wzoru: cos2x=2cos²x−1 ; cos2x=1−sin²x

	cosα+1
U{8(1−cosα)}{1+cosα)=		stąd
	cosα

9cos^α−6cosα+1=0 Δ=0

	6		1
cosα=		=
	18		3

Mila: Poprawa literówek:

8(1−cosα)		cosα+1
	=		stąd
1+cosα		cosα

9cos²α−6cosα+1=0

V.Abel: dzięki

V.Abel: Ja miałem układ pitagoras połowy trójkata , podobienstwo i warunek zadania i mi wyszło 1/9

Mila: Pewnie zrobiłeś błąd rachunkowy.

V.Abel: Już mam W proporcji jest Poprawiłem, faktycznie 1/3 Dzięki

Mila: No to pięknie.