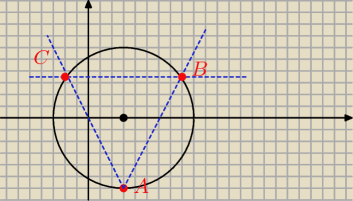
geometria analityczna matsan: Prosze o pomoc....Dany jest okrąg o równaniu (x−3)²+y²=36 .Punkt A (3,−6) jest wierzchołkiem trójkata rownobocznego ABC wpisanego w ten okrag. Wyznacz wspolrzedne wierzcholkow B i C

matsan:

	2
r=6 S=(3,0) a r to jest		h czyli h=9 nie wiem ...dalej z pitagorasa
	3

matsan: moge obliczyc dlugosc boku trojkata wyszło chyba 10 ale pozniej jak wykorzystac to do znalezienia wspolrzednych punktów?/ prosze o pomoc!

aniabb: prosta AB y=√3x−12 prosta AC y=−√3x

aniabb: wstaw rownanie prostej do okręgu wyjda współrzędne punktów

matsan: Dzięki Ania! Jesteś cudowna niezastąpiona bedę Cię ubóstwiał po wieki wieków

irena_1: Środek okręgu to punkt (3, 0), promień ma długość 6. x− długość boku trójkąta

2
	*{x √3}{2}=6
3

x √3=18 x=6√3 B=(a, b) Punkt B leży na okręgu, więc 1) (a−3)²+b²=36 oraz 2) |AB|=6√3 √(a−3)²+(b+6)²=6√3 (a−3)²+(b+6)²=108 Po odjęciu stronami obu równań: (b+6)²−b²=72 b²+12b+36−b²=72 12b=36 b=3 (a−3)²+3²=36 (a−3)²=27 a₁=3√3 lub a₂=−3√3 B=(3√3; 3), C=(−3√3; 3)

matsan: thanks irena

matsan: liczyłem niby to samo tzn długośc boku trojkata z pitagorasa i wyszlo 10 a ze wzoru R=a*√3/3 wychodzi dobrze ;s