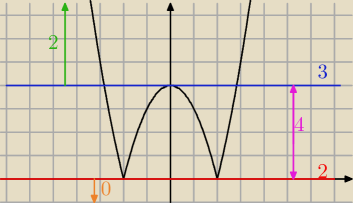
Równania z parametrem Bajka: Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m: |x²−4|=m²+3 Narysowałam wykres funkcji |x²−4|. Wyznaczyłam miejsca zerowe to x=−2 oraz x=2. Wierzchołek paraboli po odbiciu spod OX do góry to (0;4). Czy mógłby mi ktoś łopatologicznie wytłumaczyć, jak rozwiązuje się prawą stronę równania.

konrad: no to masz: m²+3<0 → brak rozwiązania 4>m²+3>0 → 4 rozwiązania m²+3>4 → dwa rozwiązania no i teraz tylko wyznaczyć w każdym przypadku m

Maslanek: Ja to bym dziabnął tak: |x²−4|= 1) x²−4 dla x∊R\(−2,2) 2) 4−x² dla x∊(−2,2) Wtedy: 1) x²−4=m²+3 m²=x²−7 m₁=√x²−7, m₂=−√x²−7 m₁=m₂ ⇔ x²−7=0 ⇒ x=√7 lub x=−√7 (które mieszczą się przedziale wyżej) m'y są określone dla x∊R\(−√7,√7) 2) 4−x²=m²+3 m²=1−x² m₃=√1−x², m₄=−√1−x² m₃=m₄ ⇔ x=1 lub x=−1 (które również mieszczą się w przedziale wyżej) m określone są dla: x∊<−1,1> Zatem: 4 rozwiązania dla m∊<−1,1) 3 rozwiązania dla m=1. 2 rozwiązania dla m∊(−∞,−√7>∪<√7,∞) Ale to nie wiem czy do końca dobrze. raczej nie Powin no się wyznaczyć iksy, ale już nie mam siły. Idę przepisywać zadanka. Baj

konrad: a właśnie, dla m²+3=4 → 3 rozwiązania

konrad: a i jeszcze dla m²+3=0 są dwa rozwiązania

konrad:

Bajka: Dzięki, w końcu to zrozumiałam