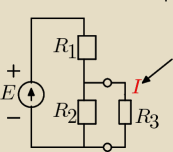
. asdf: Elektronika Potrafi ktoś obliczyć twierdzeniem Thevenina? Treść: Wykonanie pomiaru natężenia prądu I w obwodzie badanym E = 3V R₁ = 3900Ω R₂ = 1600Ω R₃=5600Ω

asdf:

asdf:

asdf: pomoze ktos?

asdf:

asdf: ?

Trivial: Spróbuję.

asdf: Ok, a dało by radę, żebyś mi to wytłumaczył?

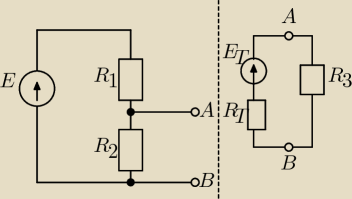
Trivial: Układ redukuje się do tego, co narysowałem.

asdf: R1 || R2?

asdf:

Trivial: A więc tak... Rozpoczynamy od policzenia oporu zastępczego R_T. Pomijamy wszelkie źródła napięcia zastępując je zwarciem (kablem) oraz wszelkie źródła prądu, które zastępujemy rozwarciem (brakiem kabla). Tutaj mamy tylko jedno źródło napięcia. Liczymy zatem... R_T = R₁+R₂. Trzeba policzyć różnicę napięcia między zaciskami A i B. Same zaciski A,B traktujesz tak jakby tam było powietrze (prąd przez nie nie płynie). Możemy oznaczyć prąd płynący przez oczko po lewej jako I_x. Stosujemy prawo Kirchhoffa dla oczka i mamy: E − I_x(R₁+R₂) = 0

	E
Ix =		(znany także jako dzielnik napięcia)
	R1+R2

Jako, że mamy już policzony prąd, który płynie przez oczko, pozostało policzyć różnicę potencjałów między zaciskami A, B. To tak, jakby policzyć różnicę potencjałów w zamalowanych kropkach. Z prawa Ohma spadek napięcia na oporniku wynosi I_xR₂, zatem... E_T = I_xR₂ Mamy już wszystko, co trzeba. Stosując analogiczną procedurę jak wcześniej do zredukowanego układu mamy:

	ET
I =		= ...
	R3+RT

Trivial: Aha i zaznaczam, że to może być źle, gdyż sam jestem w tym początkujący.

asdf: mógłbyś tu wejśc? https://secure.join.me/391-985-994

+-: Opór liczymy patrząc od trony zacisków AiB przy zwartym źródle i jest to połączenie równoległe

	R1*R2
czyli RT=		, reszta tak jak napisał Trivial się zgadza. Sumując otrzymujemy
	R1+R2

obwód zastępczy złożony ze źródła o napięciu E_T i szeregowego oporu R_T, zachowujący się identycznie jak układ pierwotny.

Trivial: Tak, +−, w linku to poprawilismy.

Trivial:

asdf: Zadanie 4: Dla E2 (wyłączamy E1):

	R1R2R3
Rz =		= 15
	R1R2 + R2R3 + R3R1

	E2		15
I4 =		=		+ U{15}[75} = 0,2A
	Rz + R4		15 + 60

	15 − 12
I3R3 = E2 − R4I4 => I3 =		= 0,75A
	40

	0,075 *40
I2R2 = I3R3 => I2 =		= 0,025A
	120

	I1R2		0,025 * 120
I1R1 = I2R2 => I1 =		=		= 0,1A
	R1		30

policzylismy I4 = E2/Rz a pozniej z oczek Dla E1:

	R1R2R2
Rz = R1 + R2 || R3 || R4 = R1 +		= 50
	R2R3 + R3R4 + R4R2

	−E1
I1 =		= −20/50 = −0,4 A = 0,4A
	Rz

	E1 − I1R1		20 − 0,4*30
E1 − I2R2 + I1R1 => I2 =		=		= 0,06(6)A
	R2		120

	I2R2
I3 =		= 0,2A
	R3

	I3 * R3
I4 =		= 0,13(3) A
	R4