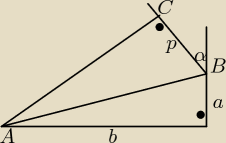
 Przedstaw za pomocą funkcji trygonometrycznych trójkąt ABC
pxcosαx b +pxsinαxa taką odpowiedź dał mi znajomy jednak nie potrafię do tego dojść. może mi to
ktoś objaśnić?
Przedstaw za pomocą funkcji trygonometrycznych trójkąt ABC
pxcosαx b +pxsinαxa taką odpowiedź dał mi znajomy jednak nie potrafię do tego dojść. może mi to
ktoś objaśnić?

| p2 | a*sinα+b*cosα | |||
P = | * | |||
| 2 | a*cosα−b*sinα |
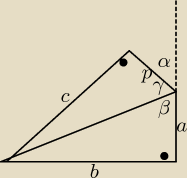
| p*c | ||
potrzebne jest mi c, bp P= | ||
| 2 |
| c | ||
tgγ = | ||
| p |
| tgα+tgβ | ||
c = p*tgγ = a*tg[180−(α+β)] = −p*tg(α+β) = −p* | = | |
| 1−tgα*tgβ |
| tgα+tgβ | ||
p* | ||
| tgα*tgβ − 1 |
| b | ||
tgβ = | ||
| a |
| tgα+ba | ||
c = p* | = | |
| ba*tgα − 1 |
| ||||||||
p* | = | |||||||
|
| a*tgα+b | a | |||
p* | * | = | ||
| a | b*tgα−a |
| a*tgα+b | ||
p* | ||
| b*tgα−a |
| |||||||||||
c = p* | = | ||||||||||
|
| ||||||||
p* | = | |||||||
|
| a*sinα+b*cosα | cosα | |||
p* | * | = | ||
| cosα | b*sinα−a*cosα |
| a*sinα+b*cosα | ||
p* | ||
| b*sinα−a*cosα |
| a*sinα+b*cosα | ||
P = p2* | ||
| b*sinα−a*cosα |