Pochodna cris93: Witam Proszę o obliczenie tej pochodnej, bo coś mi źle wychodzi:

	1
y=x−
	x2

1. Jakie będzie rozwiązanie dla tej pochodnej przyrównanej do 0? 2. Jaki będzie przybliżony wykres oraz punkt przegięcia? Pozdrawiam

cris93: Podpowie ktoś?

MQ: A co ci wychodzi?

Mila: y=x−x⁻²

	2		x3+2
(x−x−2)'=1+2x−3=1+		=
	x3		x3

Licz dalej

cris93: Zrobiłem w ten sam sposób, przyrównując do 0 wyjdzie −p³{2}

cris93: −³√2

cris93: Potem narysowałem wykres na osi jest tylko 0 oraz −³√2, linia przechodzi od góry przez ten punkt i podąża w dól ku −∞, punkt przegięcia mam właśnie w −³√2, nie wiem jak policzyc drugą wspólrzędną. Wykres jest nieprawidłowy, bo w odp są inne przedziały.

cris93: Wiem, że to już nachalnośc, ale zależy mi na tym zadaniu.

Mila:

	1
f(x)=x−
	x2

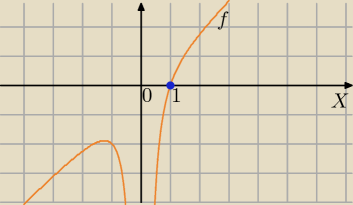
Dziedzina: x≠0

	x2−1
f(x)=
	x2

miejscse zerowe x³−1=0⇔x=1 ekstrema: f '(x)=0⇔x³+2=0⇔x=−³√2

	x3+2
f ' (x)>0 ⇔		>0⇔x<−3√2 lub x>0 (jeśli tego nie rozumiesz , to narysuj na osi)
	x3

f '(x)<0⇔x∊(−³√2;0) dla x=−³√2 jest maksimum lokalne.( wiesz dlaczego?) Co jeszcze chciałbyś wiedzieć? pisz po kolei.

cris93: Czyli tak będzie wyglądał wykres dla funkcji, ale jak dla jej pochodnej