:) radek: rownanie |x²−6x+5|=m²−5

Basia: i co z tym równaniem ?

Ann: m²≥5 ⇒m∊(−∞,−√5]∪[√5,+∞) dla takich m to rownanie ma rozwiazanie bo modul liczby zawszze jest nieujemny

radek: to jest zadanie wielokrotnego wyboru a) ma 2 rozwiązania dla m>√5 b) ma 3 rozwiązania dla m∊{−3; 3} c) ma 4 rozwiązania dla m ∊ {√5 ; 3} d) nie ma rozw dla m=2

radek:

radek: pomoze ktos

..: .

pigor: sporządzam sobie wykres funkcji y=|x²−6x+5| i widzę, że a) m >5 ⇔ m² >25 ⇔ m²−5 > 20 , więc TAK ; d) m=2 ⇔ m²=4 ⇔ m²−5=−1 , więc TAK ; a co do odpowiedzi b) lub c) nie odpowiem dopóki nie wyjaśnisz mi czy tam są nawiasy klamrowe (niedobrze gdyby tak było), czy zwykłe , bo tam piszesz średnik co by sugerowało, że to są przedziały otwarte (nawiasy zwykłe) , a nie zbiory dwuelementowe (klamrowe ) . ...

radek: tak one sa klamrowe, nie ma nawiasow

radek:

pigor: ... więc c) m=±3 ⇔ m²=9 ⇔ m²−5= 4, więc TAK ; d) m=√5 ∨ m=3 ⇔ m³−5= 0 ∨ m²−5= 4, to ma 2 lub 3 rozwiązania, więc NIE...

radek: dziekuje Ci bardzo

pigor: .. przepraszam odpowiedziałem na nie c) tylko b) i nie d) tylko c) . ...

pigor: ... , w tym ostatnim moim poście oczywiście ...

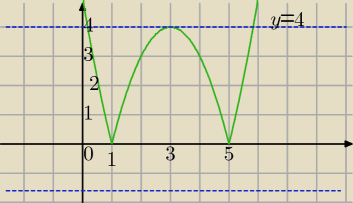
Mila: f(x)=|x²−6x+5|

	6
xw=		=3 yw=|f(3)|=|9−3*6+5|=4
	2

y=m²−5 1)a) ma 2 rozwiązania dla m>√5 F b) ma 3 rozwiązania dla m∊{−3; 3} P c) ma 4 rozwiązania dla m ∊ {√5 ; 3} P d) nie ma rozw. dla m=2 P a) sprawdzenie na rysunku: 2 rozw. dla m²−5=0 lub m²−5>4⇔ m=√5 lub m=−√5 lub m>3 lub m<−3 b) 3rozwiązania m²−5=4⇔m=3 lub m=−3 c) 4 rozw. ⇔m²−5 >0 i m²−5 <4⇔m∊(−3;−√5) lub (√5;3) wyjaśnij z nawiasami −Tak d)m²−5<0 brak rozwiązań⇔dla m∊(−√5;√5)