wart.bezw
mm: Wyznacz liczbe rozwiazań w zależności od m
I3−xI−I3+xI=m
Mam przedziały:
1.(−∞,−3) w tym przedziale dla m=6 nieskończenie wiele rozw
2.<−3,3> jedno dla m∊<−6,6>
3.(3,+∞) dla m=−6 niesk.wiele
a w odp jest inaczej że jedno jest dla m∊(−6,6)
a przedziały są:1.(−∞,−3>, 2,<3,+∞)
Skąd mam wiedzieć kiedy domknąć
10 lis 20:09
aniabb:
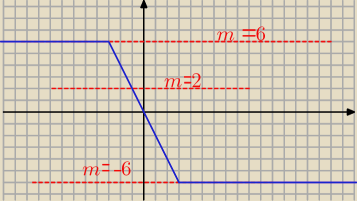
10 lis 20:12
aniabb: jak widać dla m=6 już jest ∞rozwiązań
10 lis 20:13
Basia:
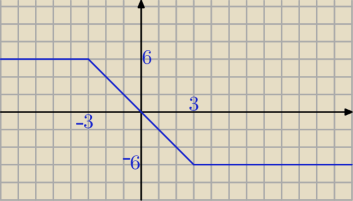
spróbuj sobie to narysować
3−x<0 ⇔ −x<−3 ⇔ x>3
3+x<0 ⇔ x<−3
x∊(−
∞,3) ⇒ L = 3−x−(−3−x) = 3−x+3+x = 6
x = <−3;3> ⇒ L = 3−x−(3+x) = 3−x−3−x = −2x
x∊(3;+
∞) ⇒ L = −(3−x)−(3+x) = −3+x−3−x = −6
z rysunku już dokładnie widać, że
dla m∊(−
∞;−6)∪(6;+
∞) nie ma rozwiązania
dla m=−6 i m=6 jest nieskończenie wiele rozwiązań
dla m∊(−6;6) jest jedno rozwiązanie
10 lis 20:18
mm: wszystko sie zgadza ale rozwiazując tylko algebraicznie i wychodząc z def wart bezw. te nawiasy
sie nie pokryją rozwiazywała juz 3 razy dopiero jak sie spojrzy na całość ale wtedy trzeba
zmienić nawiasy w przedziałach
10 lis 20:27

 spróbuj sobie to narysować
3−x<0 ⇔ −x<−3 ⇔ x>3
3+x<0 ⇔ x<−3
x∊(−∞,3) ⇒ L = 3−x−(−3−x) = 3−x+3+x = 6
x = <−3;3> ⇒ L = 3−x−(3+x) = 3−x−3−x = −2x
x∊(3;+∞) ⇒ L = −(3−x)−(3+x) = −3+x−3−x = −6
z rysunku już dokładnie widać, że
dla m∊(−∞;−6)∪(6;+∞) nie ma rozwiązania
dla m=−6 i m=6 jest nieskończenie wiele rozwiązań
dla m∊(−6;6) jest jedno rozwiązanie
spróbuj sobie to narysować
3−x<0 ⇔ −x<−3 ⇔ x>3
3+x<0 ⇔ x<−3
x∊(−∞,3) ⇒ L = 3−x−(−3−x) = 3−x+3+x = 6
x = <−3;3> ⇒ L = 3−x−(3+x) = 3−x−3−x = −2x
x∊(3;+∞) ⇒ L = −(3−x)−(3+x) = −3+x−3−x = −6
z rysunku już dokładnie widać, że
dla m∊(−∞;−6)∪(6;+∞) nie ma rozwiązania
dla m=−6 i m=6 jest nieskończenie wiele rozwiązań
dla m∊(−6;6) jest jedno rozwiązanie