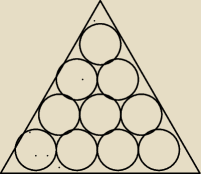
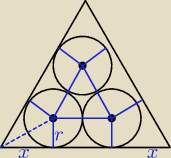
Artur z Neptuna limes granice apsik: W trójkąt równoboczny o boku a wpisano k_n okręgów o jednakowych promieniach r_k tak jak na rysunku. Niech S_kn oznacza sumę pól tych okręgów, a S oznacza pole danego trójkąta. Znaleźć granicę stosunku S_kn/S przy n→∞

	π√3
Odpowiedz to
	6

Basia:

	a2√3
S =
	4

zauważ najpierw, że liczba okręgów

	k(k+1)
nk = 1+2+3+...+k =
	2

gdzie k = liczba okręgów w pierwszym (dolnym) rzędzie dla k=2 mamy n₁ = 1+2=3 (patrz rysunek) x₂ = r₂√3 2x₂+2r₂=a 2r₂√3+2r₂ = a 2r₂(1+√3) = a

	a
r2 =
	2(1+√3)

analogicznie dla dowolnego k x_k = r_k√3 2x_k + n*2r_k = a 2r_k√3+2k*r_k = a 2r_k(k+√3) = a

	a
rk =
	2(k+√3)

	a2
Pjednego okręgu = π*
	4(k+√3)2

	k(k+1)		a2		k(k+1)a2π
Skn =		*π*		=
	2		4(k+√3)2		8(k+√3)2

Skn		k(k+1)a2π		4
	=		*		=
S		8(k+√3)2		a2√3

k(k+1)π
	=
2√3(k+√3)2

π		k2+k
	*		=
2√3		k2+2√3k+3

π√3		k2+k
	*		=
6		k2+2√3k+3

π√3		k2(1+1k)
	*		=
6		k2(1+2√3*1k + 3k2)

π√3		1+1k
	*		→
6		1+2√3*1k + 3k2

π√3		1+0		π√3
	*		=
6		1+0+0		6