awdawdawd karolajn: W urnie jest 8 kul białych i n czarnych. Z tej urny wyjmujemy 2 kule, odkładamy na bok i z pozostałych kul losujemy jedną. Prawodpodobieństwo wylosowania teraz z tej urny kuli buałej jest większe od 3/4. Wyznacz liczbę n. Rysuje drzewko i zapisuje 6+7+8/6+n > 3/4 i wychodzi mi, że należy (−6;22). W odpowiedziach są jeszcze dodatkowe założenia. Moze ktos to rozwiazac ? odp 0,1,2. Mnie wychodzi <0;22)

karolajn:

karolajn:

aniabb: rozpisać 3 przypadki ..te odłożone 2 to 1° 2 białe.. 2° 1biała 1 czarna 3° 2 czarne

karolajn: ale rozpisalem to przy drzewku, z tego po sprowadzeniu do 1 mianownika wyszlo 6+7+8/6+n

aniabb: a mi wyszło

56+7n+n2
	>3/4
6*7*8*(n+8)(n+7)

karolajn: moglabys rozpisac jak ?

karolajn:

aniabb: wszystko drzewkiem?

karolajn: tak, tylko drzewko rozumiem

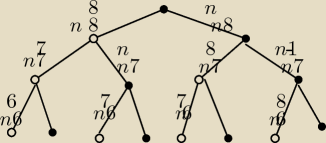
aniabb: widzę gdzie się pomyliłam

8*7*6 +8*n*7 +n*8*7 +n*(n−1)*8
	>3/4
(n+8)(n+7)(n+6)

aniabb: tam oczywiście są plusy ale w tym edytorze to obłęd

karolajn: jednak tego w ogole nie pojmuje.

aniabb: pierwsza gałązka 2 białe pierwsze potem biała

8		7		6
	*		*
n+8		n+7		n+6

druga gałązka biała czarna biała

	8		n		7
+		*		*
	n+8		n+7		n+6

trzecia gałązka czarna biała biała

	n		8		7
+		*		*
	n+8		n+7		n+6

czwarta gałązka czarna czarna biała

	n		n−1		8
+		*		*
	n+8		n+7		n+6

aniabb: czego tu jeszcze nie wiesz?

aniabb: ?

karolajn: ok, wychodzi mi 8n² + 104n +336 / (n+8)(n+7)(n+6) > 3/4 i dalej mozesz podpowiedziec co ? bo chyba gupie sie w obliczeniach i delta mi wycgodzi ujemna

aniabb: http://www.wolframalpha.com/input/?i=%288n2+%2B+104n+%2B8*7*6%29+%2F+%28%28n%2B8%29%28n%2B7%29%28n%2B6%29%29+%3E+3%2F4 n∊{0,1,2}