dawdaw karolajn: Spośród wierzchołków kwadratu o boku 2 i środków jego boków wybrano losowo dwa punkty. Oblicz prawdopodobieństwo, że odległość wybranych punktów jhest liczbą niewymierną. Wiem, że tych punktów bedzie 14, ale jak to prawidłowo zpisać, że obliczyłem ? Rysunek wyjdzie nieczytelny.

altXOR:

	8!		8*7*6!
|Ω| = C28 =		=		= 4*7 = 28 − a tyle sposobów możemy wylosować 2
	2!*6!		2*6!

punkty spośród 8 wierzchołków A −zdarzenie polegające na tym, że spośród 8 punktów trafimy na 2 takie, gdzie długość pomiędzy nimi będzie liczbą niewymierną Jak widać mamy 12 (bo kolejność losowania jest istotna − może być ten sam odcinek ale najpierw np. wylosujemy pkt A a potem B, a później możemy B, a potem A) takich możliwości (2*2 −przekątne kwadratu głównego i 2*4 odcinki łączące środki boków − 2 bo możemy na 2 sposoby wylosować pkt. na jednym odcinku), zatem: |A| = 2*6 = 12 Prawdopodobieństwo wynosi:

	|A|		12		3
P(A) =		=		=		≈ 0,43
	|Ω|		28		7

karolajn: Raczej nie. W odpowiedziach jest 1/2. Z rysunku naliczylam, nie biorąch tych samych dlugosci tak jak ty, 14.

altXOR: Chociaż masz rację, jest 14 takich długości, a kolejność nie ma tutaj znaczenia ,ważne, aby długość była niewymierna. Zatem: |A| = 14 |Ω| = 28

	14		1
P(A) =		=
	28		2

I tak zapisz...

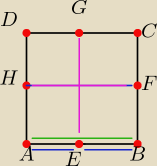
Aga1.: Wierzchołków jest 4 i środków boków jest 4 Z 8 wybierasz 2

	8 2		8*7
IΩI=		=		=28
			1*2

Łatwej policzyć, ile będzie odcinków, których długość będzie liczbą całkowitą. IA^'I=3*4+2=14 IAI=28−14=14

	IAI		1
P(A)=		=
	IΩI		2

Mila: 8 o dł.√2 4 o dl.√5 2 o dł 2√2