Stereometria tdx: zad.1 Oblicz pole powierzchni całkowitej i objętość czworościanu foremnego o wysokości 9 zad.2 Oblicz pole pow. i obj. graniastosłupa prawidłowego czworokątnego w którym długości wszystkich krawędzi wynoszą 9. zad.3 Oblicz pole pow całkowitej i obj. ostrosłupa prawidłowego sześciokątnego jeśli długość krawędzi podstawy wynosi 3 a krawędź boczna ma długość 4. 3 zadania, mam z tym problem a sprawdzian na dniach.

Kejt: 1.)

	√2
V=		a3
	12

P_c=√3a²

Kejt: a..jeszcze:

	√6
h=		a
	3

	√6
9=		a
	3

Kejt: 2) P_c=6a² a=9 P_c=6*81=... V=a³ V=9³=...

tdx: Jak przeglądam swój zeszyt to nie zauważyłem tych wzorów co podałeś przy 1 zadaniu, czy mógłbyś mi bardziej przybliżyć? H wychodzi mi 3? Nie wiem czy dobrze. No i jeszcze zadanie numer 3 do rozwiązania.

Kejt: podałaś.. te wzory wzięłam z wikipedii ale mogę Ci je wyprowadzić jeśli chcesz. H w którym zadaniu? do 3. trzeba rysunek...a ja nie znoszę rysowania tutaj sześciokątów..

tdx: Sorry nie doczytałem nicku poprzez ten rażący kolor Bardzo było by milo jak byś je wyprowadziła, H=3 wyszło mi w 1 zadaniu a w 3 to możesz jakoś same rachunki wypisać?

Kejt: 1. tutaj masz już "H" podane musisz policzyć 'a' i potem sobie wrzucić do wzorków na V i P_c okej, za chwilę to wrzucę..(trochę to może potrwać, więc pewnie dłuższą chwilę..)

Kejt:

	a√3
h=
	2

	a2√3
P=
	4

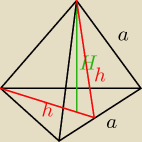
	2
spodek wysokości czworościanu foremnego dzieli wysokość podstawy na odcinki takie, że		h
	3

	1
i		h
	3

czyli: z twierdzenia Pitagorasa:

	1
H2=h2−(		h)2
	3

	3a2		1		3a2
H2=		−		*
	4		9		4

	9a2		a2
H2=		−
	12		12

	8a2
H2=
	12

	2√2a		√2a		√6
H=		=		=		a
	2√3		√3		3

zwykły wzór na objętość ostrosłupa:

	1
V=		*H*Pp
	3

1

√6

a2√3

√18a3

3√2a3

√2

V=

*

a*

=

=

=

a3

3

3

4

36

36

12

czworościan foremny składa się z czterech trójkątów równobocznych, więc:

	a2√3
Pc=4*Pp=4*		=√3a2
	4

chyba jasne? jakby co to pytaj

tdx: Dzięki za wszystko, jasne, przynajmniej wiem kiedy stosować już te ¹₃h itp.

Kejt:

	1
to		h można też wykorzystywać przy okręgach wpisanych i opisanych na trójkącie
	3

równobocznym:

	2
R=		h (opisany)
	3

	1
r=		h (wpisany)
	3

zaraz zaopiekuję się tym trzecim..

Kejt: H²=4²−3² H²=16−9 H²=7 H=√7 a=3

	a2√3
Pp=6*
	2

	1
V=		*H*Pp
	3

do pola powierzchni oblicz sobie wysokość ściany bocznej z pitagorasa(h), wtedy:

	ah
Pc=Pp+6*		=Pp+3ah
	2

dasz radę dalej?

tdx: Dam radę, dzięki.

Kejt: powodzenia na sprawdzianie