funkcje CYKLOMETYCZNE els: Hej, mam problem z nierównościami cyklom. proszę o pomoc, wskazówki arccos x/x−2< arccos (1/2), czy mogę tu podzielic obie strony przez arccos?

Artur_z_miasta_Neptuna: możesz ... ale ... zmieniając znak nierówności dlaczego bo funkcja arccos jest MALEJĄCA czyli arccos (y) > arccos (y + 'coś') (oczywiście będąc w dziedzinie arccos)

els: oki, czy mogłabym napisać rozwiazanie i sprawdzi Pan czy jest w porządku?

Artur_z_miasta_Neptuna: oczywiście ... najlepiej jeżeli napiszesz całe zadanie począwszy od założeń (bardzo ważna sprawa przy arcusach)

els: tzn? założenia czyli dziedzina, przeciwdziedzina?

Artur_z_miasta_Neptuna: założenia = dziedzina

Artur_z_miasta_Neptuna:

	x
a raczej ... jaki musi być 'x' aby		miał sens jako ułamek) i należał do dziedziny
	x−2

arcusa

els: oki, więc już się zabieram do rozwiązywania

els: to moze nie będę wszytskiego pisać tylko najogólniej...ale z sensem. Dziedziną jest przedział [−1,1] i zakładam ze moje wyrażenie x/x−2 zawiera się w tym przedziale i z pierwszego warunku wychodzi mi przedział (−∞, 1)u(2,∞) zaś z drugiego x należy od (−∞, 2)

Artur_z_miasta_Neptuna: czyli ostatecznie jaki może być 'x' i dlaczego twierdzę, że jest tylko PRAWIE dobrze

els: musi to być częśc wspólna...? czyli od −∞ do 1 przedziały otwarte

els: wiec rozwiązuje dalej

Artur_z_miasta_Neptuna: i masz niestety źle podstaw x=1

1
	= −1 ... arcos (−1) = π
1−2

Artur_z_miasta_Neptuna: a dlaczego masz źle ... bo rozwiązując wstawiłaś < zamiast ≤

Artur_z_miasta_Neptuna: dlatego napisałem PRAWIE dobrze

els: ahhh, tak! czyli (−∞, 2>

els: ale czy 2 nie odpada ze wzg ze jest w mianowniku?

Artur_z_miasta_Neptuna: ejjj ejjj ejjj spokojnie część wspólna to raz a dwa −−− mówiliśmy tylko o tym aby wyrażenie się mieściło w dziedzinie arcusa ... 2 odpada ze względu na mianownik i to jest oczywiste

els: ahhh no tak, o czym ja myśle.... czyli ostatecznie (−∞,1>?

Mila: Rozwiązałam inną nierówność, a mianowicie:

arccos x
	< arccos (1/2)
x−2

a ma być:?

	x		1
arccos		< arccos
	x−2		2

els: tak, drugą wersję mam w poleceniu

Artur_z_miasta_Neptuna: tak .. takie jest założenie co do x

els: oki, ostateczny wynik wyszedł mi (−∞,0)u(2,4) a powinno być <−2,0)(odpowiedzi)... mogłby Pan rozwiązać...? bo ja piszę to i pisze i cay czas tak samo...

Artur_z_miasta_Neptuna: a możesz pokazać jak rozwiązywałaś/−eś

Artur_z_miasta_Neptuna: krok po kroku i jak Ci mogło wyjść x>1 skoro x∊(−∞,1> <−−−− założenie

els: x/x−2>x/2 przeniosłam, sprowadziłam do wspólnego mianownika... i ptrzymałam 2x−x²+2x/(2x−4)>0 podniosłam do kwadratu i otrzymałam (−x²+4x)(2x−4)>0 itd

els: no to muszę źle myśleć... ale już kombinuje i kombinuje i nic

Artur_z_miasta_Neptuna:

x		1
	>
x−2		2

2x − x + 2
	> 0
2(x−2)

2(x+2)(x−2) > 0

els: a dlaczego zniknął "x" prz 1/2?

Artur_z_miasta_Neptuna: bo tak na samej górze jest podane ... patrz pierwszy post

els: jejku...ja go zgubiłam przy przepisywaniu przykładu z książki! przepraszam!

Artur_z_miasta_Neptuna:

	x
to jeszcze nie kończyłaś założenia ...		∊<−1;1> ... czyli x∊<−2;2>
	2

więc z założeń wynika, że rozpatrujesz tylko x∊<−2;1>

els: ah, tak! teraz się wszystko zgadza, dziękuję za pomoc, mam jeszcze tylko pytanie. znak w nierownosciach cyklom. zmieniamy gdy mamy do czynienia z arcsin, arccos i arcctg?

Artur_z_miasta_Neptuna: i teraz sama nierówność

x		x
	>
x−2		2

x(2−(x−2))
	> 0
2(x−2)

x(4−x)(x−2) > 0 −x(x−2)(x−4) > 0 x(x−2)(x−4) < 0 szkic wielomianu wykonaj i wychodzi, że x∊(−∞;0)∪(2,4) po uwzględnieniu założeń wychodzi

els: tak, tak, przeanalizwoałam wszystko i zgadza się.

Artur_z_miasta_Neptuna: arcsin −−− funkcja rosnąca ... im wieksza wartość pod arcusem tym większy arcus −−− znak niezmieniony arccos −−− funkcja malejąca ... dalej domyślasz się co będzie arctg −−− funkcja rosnąca arcctg −−− funkcja malejąca wystarczy taka odpowiedź zajrzyj do wykresów tychże funkcji

els: a jeszcze jedno pytanko... jak potraktować wyrazenie |arcsin2x| w nierównościach?

Mila: D:

	x
−1≤		≤1 ⋀ x≠2⇔
	x−2

x		x
	≥−1 ⋀		≤1 ⋀ x≠2⇔
x−2		x−2

x		x
	+1≥0 i		−1≤0 i x≠2
x−2		x−2

x+x−2		x−x+2
	≥0 i		≤0 ⇔
x−2		x−2

2x−2		2
	≥0 i		≤0⇔
x−2		x−2

x≤1lub x>2 i x<część wspólna x∊(−∞;1>

Artur_z_miasta_Neptuna:

	x		1
Mila ... oraz		zamiast		jest w drugim arcusie
	2		2

Mila: No to już nie liczę, bo pytałam jaka treść. Drugą część dziedziny już łatwo .

els: a jak z tym arcsin2x zrobić?

Mila: a jaką masz nierówność?

els: |arcsin2x|≥π/3

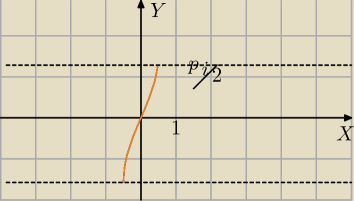
Mila: dziedzina jak zwykle.

	π		π
−		≤arcsin2x≤
	3		3

działaj dalej sama

els: przedziały to wiem.. ale co konkretnie mam zrobić z tą dwójką w arcsin2x

Mila: Oj, podałam Ci rozwiązanie dla

	π
|arcsin(2x)|≤
	3

Teraz

	π
|arcsin(2x)|≥		⇔
	3

	π		π
arcsin(2x)≤−		lub arcsin(2x)≥
	3		3

Zaraz podpowiem dalej.

els: oki jeszcze młoda godzina

els: oki jeszcze młoda godzina

Mila: 2x=u arcsinu=α ⇔ u=sinα

	π		π		π		π
α≤−		i α≥−		lub α≤		i α≥
	3		2		2		3

	π		π
sinx jest rosnący w przedziale<−		;		>
	2		2

	√3
sinα≤−		i sinα≥−1lub .....
	2

dokończysz?

els: juz juz próbuje ogarnać to

Mila: Dobranoc, z Arturkiem czekamy na podziękowanie.

els: Oczywiście, dziekuję ślicznie!