parametry Ela: dla jakich m równanie x²−4|x|+m²−5=0 ma dwa różne rozwiązania ? odpowiedź ma być m∊{−3,3} suma (−√5, 5)

Jack: zauważ, że funkcja jest parzysta, wystarczy znaleźć jeden pierwiastek dodatni dla funkcji bez modułu... Na oko (więc mogę się mylić) powinny wyjść konkretne wartości m, a nie przedział. Na pewno chodzi o DWA różne rozwiązania, a nie cztery?

ela: tak, o dwa. Tak jest w treści zadania. Ja zrobiłam tak, że najpierw postawiłam warunki : gdy x≥0 funkcja ma postać x²−4x+m²−5=0 gdy x<0 x²+4x+m²−5=0 potem wyliczyłam delty każego z tego równania i miejsca zerowe (delta oczywiście większa od zera) ale nie wyszło. moglby mi ktos to poprawnie rozwiązać ?

ZKS: Narysuj jedną funkcję y = |x|² − 4|x| − 5 i y = −m² (prosta pozioma do OX)

Jack: a ok, widzę: − dla x²−4x+m²−5=0 przyjmuj założenia: Δ>0 i x₁*x₂<0 lub Δ=0 i x₁=x₂>0

ela: a mój poprzedni sposób jest zły . ?

Jack: dobry. Tylko pamiętaj, że szukasz tego w zawężonej dziedzinie, więc oba pierwiastki raz powinny być dodatnie, a drugim razem ujemne.

ela: bo mi pierwszy zbiór wyszedł (−3, 3) a nie x∊{−3, 3 } i właśnie nie wiem ,co źle zrobiłam . może napisze co zrozbłam z pierwszym warunkiem( analogicznie drugi rozpatrzyłam tak samo ) Δ= −4m²+36 Δ>0 −4m²+36>0 Δm=576 m1=3 m2=−3 wówczas wychodzi przedział (oczywiście z popredznim uwzględnieniem że x≥0) m∊ (−3,3)

dragon: ale dwa różne rozwiązania to nie oznacza, że one mają być różnych znaków, więc w tym zadaniu wystarczy tylko założenie o delcie

ZKS: −4m² + 36 > 0

	1
−4(m2 − 9) > 0 / * (−		)
	4

(m − 3)(m + 3) < 0

dragon: ponieważ ta funkcja jest parzysta to przy delcie =0 będą dwa różne rozwiązania. jedno dodatnie jedno ujemne

ela: i co w związku z tym ZKS ? czy cos zrobiłam niepoprawnie ? widze, że u Ciebie jest inny znak ..

ZKS: 1^o Δ = 0 2^o Δ > 0 ∧ x₁x₂ < 0

ela: a nie przepraszam, z Twoich obliczeń również wynika, że m∊(−3,3) ....

dragon: można rozpatrywać jeden przypadek po stwierdzeniu, że fun jest patrzysta i należy zrobić założenie, że delta = 0 albo rozpatrzyć dwa przypadki x≥0 i x<0 i robić założenie, że delta = 0

ela: ale to nie mają być różne pierwiastki ( PRZECIWNYCH ZNAKÓW ) tYLKO RÓŻNE PIERWIASTKI, A WIĘC tak jak powiedział dragon tamte zalożenia nie są potrzebne ... przynajmniej ja tak mysl,e , jesli jestem w błedzie to przepraszam, ale prosze o wytłumaczenie mi tego dlaczego tak jest...

dragon: ZKS pisze źle

ZKS: Może i nie myślę już więc napisz dragon odpowiedź.

ela: dragon, bardzo Cię proszę, napisz mi chociaż początek tego zadania. ponieważ dalej tego nie rozumiem... gdybym dostała to na sprawdzianie, to rozpatrywałabym te dwa przpadki, jak napisałam wyżej i założyłabym, że Δ>0( bo jak sie uczyłam wtedy są dwa RÓŻNE pierwiastki )

dragon: co konkretnie mam Ci wytłumaczyć?

dragon: odp m = 3 lub −3

ela: Mimo wszystko, ZKS, dzięki za chęć pomocy. Pora nie jest odpowiednia na myślenie

ZKS: Tylko m = ±3?

ela: dlaczego jest tak, że Δ=0 ( bo ja to biore dosłownie, że dwa pierwiastki róże czyli Δ>0 nierozumiem tego, dlaczego jesli funkcja jest parzysta to Δ musi sie równać zero . ( wsydliwie sie przyznając nie pamietam nawet jak wyglada przykład wykresu funkcji parzystej )

ela: Nie, ZKS, ustalamy teraz dopiero pierwsze założenie

dragon: no tylko prosta równoległa do osi będzie się stykać z "parabolą " w wierzchołku po dwóch stronach osi Y (bo fun jest parzysta)

ela: coś kojarze że moz.e to być wykres fukcji, którego osią symetry jest os oy, choć moge sie bardzo mylić ..

ZKS: To co masz po prawej stronie OY odbijasz na lewą stronę.

dragon: funkcja parzysta jest symetryczna względem osi y, więc delta =0 da w każdym przypadku po jednym rozwiązaniu co razem złoży się na dwa rozw.

ZKS: Myślałem że wywnioskowaliście że rozwiązaniem jest tylko m = ±3 co nie jest prawdą.

ela: kurcze, dalej nie rozumiem tego. hmm z drugiego załozenia wynikaloby że m∊(−√5, 5) jesli zatem delta wynosiła by zero, to były tylko zbiór dwuelementowy ... nieprawdaż ?

ela: jeśli miałby ktos czas to bardzo bym prosiła o całe rozwiazanie tego zadania tym sposobem , który ja proponuje ...

ZKS: Zauważ dla Δ > 0 dostaniemy dwa pierwiastki ale jeżeli nałożymy na to warunek że mają być różnych znaków jeden nam odpadnie z parzystości. Dla x ≥ 0 x² − 4x + m² − 5 = 0 Δ = −16 − 4m² + 20 m² − 9 < 0 ⇒ m ∊ (−3 ; 3) Dla tych m będziemy dostawać dwa pierwiastki jeżeli obydwa będą większe od 0 będziemy musieli odbić je na lewą stronę więc dostaniemy w sumie cztery pierwiastki natomiast nakładając warunek x₁x₂ < 0 będziemy mieli jeden dodatni drugi ujemny więc ten dodatni tylko odbijemy na lewą stronę i wtedy dostaniemy dwa pierwiastki bo pierwszy nam odpadnie. Rozumiesz?

ZKS: Jeżeli źle piszę to dragon niech mnie poprawi.

ela: tylko zę to mają być dwa różne pierwiastki np. 2,3 lub −1, 2 i widac ze one niekoniecznie musza byc różnoimienne

ZKS: A czy −2 i 2 to są różne pierwiastki czy nie?

dragon: ZKS pisze żle

ela: moim zdaniem tak

dragon: wystarczy tylko warunek aby Δ=0

ZKS: Według Ciebie jak jest odpowiedź napisz dla jakich m jest to spełnione?

dragon: dla m = 3 lub −3

ela: napisałam ponizej tresci zadania zrozwiązanie

ela: ale to tylko 1 załozenie jeszcze do rozpatrzenia drugie

ela: a potem suma tych dwóxch

ZKS: Zrozum człowieku że dla Δ = 0 będzie za mało. Dam Ci przykład. Dla m = 1 (nie należy do warunku Δ = 0) dostajemy: x² − 4|x| − 4 = 0 a rozwiązaniem tego równania jest x = ±2(1 + √2) są dwa są a Ty piszesz że tylko dla Δ = 0 to zajdzie.

Piotr: dragon ŹLE podstaw sobie np 0 i sprawdz

ZKS: Widzisz o co mi chodzi ela?

dragon: oba założenia nie mają wpływu na m, bo założenie robimy dla x: x≥0 i x<0 w obu przypadkach otrzymujemy to samo zrób sobie sprawdzenie zadania i podstaw za m np. 3 i narysuj albo rozwiąż i się przekonasz, że będą dwa rozw.

ZKS: Przez człowieka na początku aż zwątpiłem w siebie może rzeczywiście jakąś bzdurę pisze myślałem. Dzięki Piotr za wsparcie.

ZKS: A Ty się przekonaj że dla m = 0 ; m = 1 ; m = 2 dostajemy dwa pierwiastki.

ela: no napewno to jest analogiczne do tego co przedtem napisałes. jednak nie rozumiem tego dalej.. ale wlasnie tego potrzebowała wykresu, z racji tego ze jestem wzrokowcem .. jesli jeszcze raz ZKS MOZESZ MI TO wytłumaczyc, to bede wdzieczna .

Piotr: nie ma sprawy ZKS. czekalem czy dragon dopisze cos jeszcze ale widze, ze upiera sie przy swoim

dragon: zostałem pokonany, przegrałem przepraszam za zamieszanie, przyznaję rację, oddaję honor ZKS nie gniewaj się, jesteś świetny

ZKS: x² − 4|x| + m² − 5 = 0 Rozpisujemy na przypadki x ≥ 0 x² − 4x + m² − 5 = 0 Δ = 16 − 4m² + 20 m² − 9 > 0 ⇒ m ∊ (−3 ; 3) [dla tych m mamy dwa różne pierwiastki] jeżeli te dwa pierwiastki będę większe od 0 to spełnią warunek x ≥ 0 i będziemy musieli je obić na drugą stronę (wynika to z parzystości funkcji) więc w sumie dostaniemy cztery różne pierwiastki a my potrzebujemy tylko dwóch więc musimy zadbać o to aby jeden pierwiastek był większy od 0 wtedy spełni warunek x ≥ 0 a jeden pierwiastek był mniejszy od 0 i nie spełni nam warunku x ≥ 0 (wtedy nie odbijemy jego na lewą stronę tylko tego który jest dodatni) a tylko wtedy będziemy mieli to kiedy spełnią warunek x₁x₂ < 0.

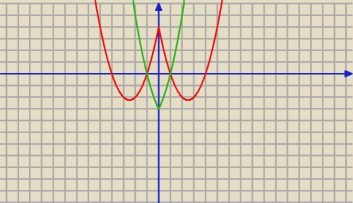
ZKS: I ten rysunek się właśnie tego tyczy co napisałem teraz

	4
y = x2 − 5|x| + 4 warunek x1x2 =		więc obydwa pierwiastki dodatnie odbijamy na
	1

lewą stronę i mamy w sumie cztery pierwiastki co widać na rysunku.

	−3
Następnie y = x2 + 2|x| − 3 warunek x1x2 =		więc jeden dodatni jeden ujemny
	1

na lewą stronę odbijamy tylko dodatni pierwiastek i otrzymujemy dwa pierwiastki. czerwony wykres oraz zielony wykres na rysunku

ZKS: Mam nadzieję że w miarę jasno to wyjaśniłem i napisałem jak jeszcze coś jest nie zrozumiałe pisz ela to postaramy wytłumaczyć.

ela: powracajac do wczorajszego tematu.... zrobiłam pierwszy warunek metodą graficzną niestety przy drugim warunką są schody ponieważ mi nie wychodzi . pomoże ktoś ?

ela: podzieliłam to na dwie funkcje x²−4|x|−5 oraz drugą −m² niestety nie wychodzi mi przy oliczeniach drugiej

pigor: ... ja podsumowując waszą dyskusję ... widzę to tak : dane równanie x²−4|x|+m²−5=0 spełnia warunki zadania ⇔ |x|²−4|x|=5−m² /+4 ⇔ ⇔ |x|²−4|x|+4=9−m² ⇔ (|x|−2)²=9−m² ⇔ ⇔ (9−m²=0 i |x|−2=0) lub (9−m²>0 i ||x|−2|=√9−m²) ⇔ ⇔ (|m|=3 i |x|=2) lub (|m|<3 i |x|−2=−√9−m²) lub (|m|<3 i |x|−2=√9−m²) ⇔ ⇔ (*) m=±3 lub (|m|<3 i |x|=2±√9−m² i 2−√9−m²>0) ⇒ ⇒ |m|<3 i √9−m²< 2 ⇔ |m|<3 i 9−m²< 4 ⇔ |m|<3 i |m|>√5 ⇔ ⇔ −3< m<3 i (m<−√5 lub m>p{5{) ⇔ −3< m<−√5 lub √5< m<3, to stąd i z (*) ⇔ m∊<−3;−√5) U (√5;3> − szukany zbiór wartości m ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− no cóż pisałem on−line i być może źle coś ogarnąłem (zinterpretowałem) , bo nie wyszło mi tak jak miało być, ale może niech ktoś tego "coś" poszuka, dziękuję . ...