Znajdź wartości dla x
Lenka: 7x2=2x3+9
9 lis 11:00
aniabb: dla −1 jest spełnione i horner
9 lis 11:02
Lenka: a mogłabym prosić o rozpisanie tego byłabym bardzo wdzięczna
9 lis 11:03
aniabb: albo 2x3+2x2 −9x2+9 =0
9 lis 11:03
Lenka: dziękuje za pomoc jednak nadal nie bardzo to dla mnie zrozumiałe
9 lis 11:06
aniabb:
2x2(x+1) −9(x2−1)=0
2x2(x+1) −9(x−1)(x+1)=0
(x+1)(2x2−9x+1) =0 deltę sama
9 lis 11:07
irena_1: 2x
3−7x
2+9=0
2x
3+2x
2−9x
2+9=2x
2(x+1)−9(x
2−1)=2x
2(x+1)−9(x+1)(x−1)=(x+1)(2x
2−9x+9)
(x+1)(2x
2−9x+9)=0
x
1=−1 lub 2x
2−9x+9=0
Δ=81−72=9
| | 9−3 | | 9+3 | |
x2= |
| =1,5 lub x3= |
| =3 |
| | 4 | | 4 | |
9 lis 11:07
Lenka: i wszystko jasne dziękuje i pozdrawiam
9 lis 11:07
Lenka: dziękuje za rozwiązanie a teraz czy ktoś byłby w stanie mi wyjaśnić dlaczego nagle w
rozwiązaniu Pani aniabb ginie 7
9 lis 11:21
aniabb: bo −7 = 2 − 9
9 lis 11:29
Lenka: dla −1 jest spełnione to można wyliczyć mówiąc kolokwialnie "w głowie" jednak jest możliwość
wyprowadzenia tego z pomocą wzoru?
Czy byłaby Pani w stanie przedstawić to za pomocą hornera?
9 lis 11:39
Lenka: Przepraszam wklejona pierwsza wiadomość temat uważam za zamknięty wszystkim serdecznie dziękuje
za zainteresowanie moją sprawą.
Pozdrawiam serdecznie
9 lis 11:44
aniabb:
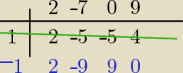
szukamy wśród podzielników wyrazu wolnego 1,−1,3,−3,9,−9
pasuje −1 i mamy (x+1)(2x
2−9x+9)=0
no fakt u siebie zapomniałam w ostatniej linijce 1*9
9 lis 11:47
Lenka: Jeszcze raz dziękuje
9 lis 12:01
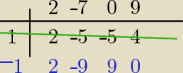 szukamy wśród podzielników wyrazu wolnego 1,−1,3,−3,9,−9
pasuje −1 i mamy (x+1)(2x2−9x+9)=0
no fakt u siebie zapomniałam w ostatniej linijce 1*9
szukamy wśród podzielników wyrazu wolnego 1,−1,3,−3,9,−9
pasuje −1 i mamy (x+1)(2x2−9x+9)=0
no fakt u siebie zapomniałam w ostatniej linijce 1*9