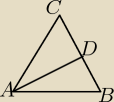
Prosze o pomoc pitt: 1. Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym AC=BC. Odcinek AD dzieli trójkąt ABC na dwa trójkąty równoramienne w taki sposób że AB=AD=CD. oblicz miary kątów trójkąta ABC. (patrz rysunek powyżej) 2. Oblicz pole trójkąta równoramiennego ABC, w którym AB=24 i AC=BC=13. 3. Liczby 4, 10, c są długościami noków trójkąta równoramiennego. Oblicz c.

tim: 3. Jest banalne przecież: Żeby był równoramienny c ∊ {4,10} Ale jest założenie. Aby trójkąt powstał trójkąt musi być spełniona zależność: a + b > c a + c > b b + c > a Sprawdzamy: 4 + 10 > c 4 + c > 10 10 + c > 4 Wynika z tego, że c > 7 Czyli jedyny wariantem jest c = 10.

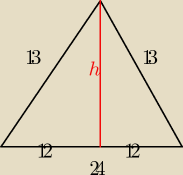
tim: 2. Skorzystaj z wzoru Herona, jeżeli nie znasz to z Pitagorasa i liczysz h.

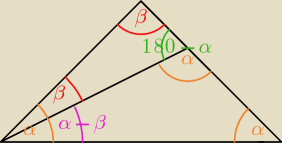
tim: Tak mieszczą się kąty I mamy układ równań: α + α + (α − β) = 180 β + β + (180 − α) = 180 Wystarczy rozwiązać.

tim: Można tez dodać α + α + β = 180

pop: 2α+(α−β)=180 2β+(α−180)=180