Oblicz pola i objetości pralinka.: 1. Ściany boczne ostrosłupa prawidłowego czworokątnego są trójkątami równoramiennymi o podstawie 6 i ramionach 12. Oblicz miarę kąta między przeciwległymi ścianami bocznymi tego ostrosłupa. Oblicz objętość tego ostrosłupa. 2. Przekątna graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a promień okręgu opisanego na podstawie 3 cm. Oblicz objętość i pole powierzchni całkowitej graniastosłupa. 3. W ostrosłupie prawidłowym trójkątnym krawędź boczna długości 8 dm jest nachylona do płaszczyzny podstawy pod kątem 60°. Oblicz pole powierzchni bocznej i objętość tego ostrosłupa. Proszę o rysunki i zadania.

dero2005: a = 6 l = 12 h_s = √l² − (^a₂)² = √12²−3² = √144−9 = √135 = 3√15 a² = h_s²+h_s²−2h_s*cosα 6² = (3√15)³+(3√15)²−2*(3√15)²*cosα 36 = 135+135 − 270*cosα

	270−36		√780
cosα =		=		≈ 0,8666
	270		30

α≈30^o d = a√2 = 6√2 h = √l² − (^d₂)² = √12² − (3√2)² = √144 − 18 = √126

	a2*h		62*√126
V =		=		= 12√126
	3		3

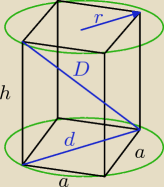
dero2005: D = 8 r = 3 d = 2r = 6 a = U{d√2{2} = 3√2 h = √D² − d² = 2√7 V = a²*h = 36√7 P_c = 2a² + 4a*h = 12(3+2√14)

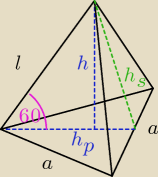
dero2005: l = 8

2   hp 3		1
	= cos 60o =		→ hp = 6
l		2

	2
a =		√3hp = 4√3
	3

h_s = √l² − (^a₂)² = 2√13

h		√3
	= sin 60o =		→ h = 4√3
l		2

	a2√3
Pp =		= 12√3
	4

	Pp*h
V =		= 48
	3

	3
Pb =		a*hs = 12√39
	2

Eta: dal specjalisty od stereometrii