
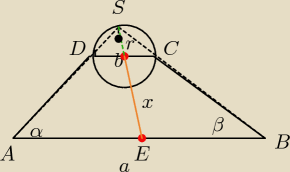
 α+β=900 ⇔Kąt ASB=900
Promień okręgu opisanego na Δ prostokątnym jest równy połowie przeciwprostokątnej
α+β=900 ⇔Kąt ASB=900
Promień okręgu opisanego na Δ prostokątnym jest równy połowie przeciwprostokątnej
| 1 | ||
r= | b promien okręgu opisanego na ΔDCS | |
| 2 |
| 1 | ||
R=SE= | a promien okręgu opisanego na ΔABS | |
| 2 |
| 1 | 1 | 1 | ||||
x=SE−r= | a− | b= | (a−b) | |||
| 2 | 2 | 2 |
 dzięki wielkie
acz rozkminilem to w miedzy czasie inny sposobem.
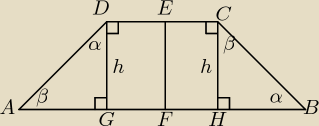
Kąt CBH to α, a kąt DAG to β. α + β = 90. Opuszczone wysokości tworzą nam trójkąty. Istotnie
dzięki wielkie
acz rozkminilem to w miedzy czasie inny sposobem.
Kąt CBH to α, a kąt DAG to β. α + β = 90. Opuszczone wysokości tworzą nam trójkąty. Istotnie
| a − b | ||
kąt BCH to β, a kąt ADG to α. Wynika, że AG = h = BH = | = EF. | |
| 2 |
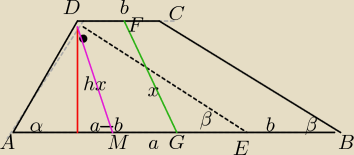 II sposób
DE||CB
AE=a−b
W ΔAEG:
II sposób
DE||CB
AE=a−b
W ΔAEG:
| AD | ||
sinβ= | ||
| a−b |
| a−b | ||
AM= | ||
| 2 |

