fk xyz: oblicz najwieksza i najmniejsza wartosc funkcji kwadratowej f(x)=(2x+1)(x−2) w przedziale <−2;2>. wiem jak to zrobic rysujac wykres ale w poleceniu jest oblicz proszę o pomoc

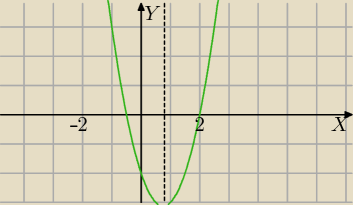
Mila: f(x)=(2x+1)(x−2)⇔f(x)=2x²−4x+x−2 f(x)=2x²−3x−2 badamy czy wierzchołek paraboli należy do danego przedziału

	3
xw=		∊<−2;2> zatem najmniejszą wartość ma funkcja w wierzchołku paraboli
	4

	−25
yw=		wartość najmniejsza danej funkcji
	8

największa wartość w końcu przedziału bardziej oddalonego od x_w. f(−2)=... wartość największa tej funkcji w przedziale <−2;2> zadanie rozwiązujemy bez rysunku, rysunek tylko dla sprawdzenia.

Mila: Tego typu zadanie jest na każdej maturze.

Gustlik: Można tak − p i q wyliczamy z pominięciem postaci ogólnej:

	1
f(x)=(2x+1)(x−2) ⇔ x1=−		, x2=2
	2

	x1+x2		1   − +2   2		3
p=		=		=
	2		2		4

	3		3		3		5		−1		25
q=f(p)=f(		)=(2*		+1)(		−2)=		*		=−
	4		4		4		2		4		8