Zbadaj okresowość funkcji. ss: Zbadaj okresowość funkcji: a) f(x) = sin²x

	x
b) f(x) = tan(		)
	2

	sin2x
c) f(x) =
	cos3x

d) f(x) = tan6x + cos3x e) f(x) = arccosx Proszę, niech mi ktoś wytłumaczy jak to zrobić. Pozdrawiam! Prosiłbym tak ładnie, kroczek po kroczku..

ss: Pomoze ktoś?

Mila: Teraz tylko wskazówka, bo zaraz musze zwolnić komputer. np. f(x)=sin(2x) sin2(x+T)=sin2x wyznacz T, ma być niezależne od x

Mila: Co, to? Nic nie zrobione?

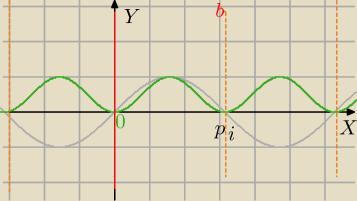
Mila: Graficznie: y=sinx popielaty y=sin²x zielony T=π okres zasadniczy Podaje się też kπ; k∊C Obliczanie sin²(x+T)=sin²x T≠0 sin²(x+T)−sin²x=0 (sin(x+T)−sinx)*(sin(x+T)+sinx)=0 rozwiąż warunek, skorzystaj, że sinx ma okres zasadniczy 2π)

	x+T		x
b) tg(		)=tg		funkcja tgx jest okresowa , zatem
	2		2

	x+T		x		x+T		x
tg(		)=tg(		+kπ)⇔		=		+kπ⇔
	2		2		2		2

x+T=x+2kπ⇔T=2kπ, k∊C okres zasadniczy T=2π