Pytanko o brak parzystości i nieparzystości. ss: Witam! Mam pytanko co do parzystości i nie parzystości funkcji. Funkcja jest nieparzysta kiedy f(−x) = −f(x) Parzysta kiedy f(−x) = f(x) Ale wiem, że jest też coś takiego jak brak parzystości i nieparzystości, natomiast niewiem jak to się objawia. Czy ktoś wytłumaczyłby mi to bądź pokazał na jakimś konkretnym przykładzie? Pozdrawiam!

Artur_z_miasta_Neptuna: tym że nie zachodzi ani jedna ani druga równość

Artur_z_miasta_Neptuna: np. (x−1)² nie jest parzysta i nie jest nieparzysta

ss: Odrazu dorzucę pytanko. Mam zbadać parzystość funkcji:

	π
f(x) = sin(		− x )
	2

	π
I mam to rozpisane. Podstawiam za x (− x) i otrzymuję f(−x) = sin(		+ x} a dalej jest to
	2

	π
rozpisane ( i tu tego nie rozumiem) sin(π −(		+ x )
	2

Nie rozumiem co tu się stało. Pozdrawiam. Proszę o pomoc

ss: Artur a mógłyś mi to jakoś rozpisać? Bo Cięzko mi sobie wyobrazić, że nie zachodzi ani jedna ani druga równość. Nawet na podanym przez Cb przykładzie cieżko mi to skumać. bo jak nie wychodzi mi f(x) ani −f(x) no to co mi wtedy wyjdzie?

konrad: jak nie zachodzi ani jedna ani druga równość no to f. nie jest ani parzysta ani nieparzysta

ss: konrad. W teorii to rozumiem ale w praktyce nie.

ss: Dla przykładu:

	x+1
Mam funkcje f(x) =		− wiem, że jest to funkcja ani parzysta ani nie parzysta.
	x−1

Ale niewiem jak to udowodnić. Mogły mi ktoś to rozpisać?

konrad: x≠1 ⇒ D:x∊R\{1} ⇒ dziedzina nie jest symetryczna względem zera, zatem f. nie jest parzysta ani nieparzysta

Artur_z_miasta_Neptuna: zacznijmy od przeksztalcenia f(x)

	x+1		x−1 + 2		2
f(x) =		=		= 1 +
	x−1		x−1		x−1

	2		2
f(−x) = 1+		= 1 −
	(−x) − 1		x+1

	2
−f(−x) = −(1 −		)
	x+1

czy parzysta f(x) ?=? f(−x)

	2		2
1 +		= 1 −
	x−1		x+1

1		1
	= −
x−1		x+1

x+1 = −(x−1) x+1 = −x + 1 x = −x x = 0 ... tylko dla takiego x zachodzi ... czyli nie jest parzysta czy jest nieparzysta

	2		2
1 +		= −1 +
	x−1		x+1

	2		2
2 +		=
	x−1		x+1

	1		1
1 +		=
	x−1		x+1

x−1+1		1
	=
x−1		x+1

x		1
	=
x−1		x+1

x(x+1) = x−1 x² + x − x + 1 = 0 x²+1 = 0 <−−− nie jest prawdą dla żadnego 'x' czyli f(x) nie jest nieparzysta

Artur_z_miasta_Neptuna: o kurdę ... zapomniałem o dziedzinie

ss: czekaj bo najpierw napisałeś dziedzinę i na jej podstawie określiłeś, że funkcja jest nieparzysta. Jakby wyglądała dziedzina gdyby funkcja była parzysta? 1 i − 1 ?

konrad: dziedzina musi być symetryczna względem zera by f. była parzysta lub nieparzysta czyli np. R\{−1,1}

ss: aha. Czyli na dobrą sprawę sprawdzam najpierw dziedzinę. Jeżeli liczby z tej dziedziny są przeciwne jak np. (−1,1) to wiem, że funkcja jest parzysta lub nieparzysta i wtedy sprawdzam. A jak jest samo (np. −1) to nie jest ani parzysta ani nie jest nie parzysta, tak? a jak jest D:R/{ −1,1,5} to co wtedy?

ss: Nie rozumiem też skąd artur sprawdzając parzystość wziął :

1		1
	= −
x−1		x−1

W sensie znaki kumam. Niewiem skąd wzieło mu się to jeden w liczniku.

konrad: D:R/{ −1,1,5} ⇒ żadna

konrad: co do rozwiązania Artura, nie chce mi się wnikać

ss: a Ty jakbyś to sprawdził konrad jeśli nie dziedziną?

konrad: co? nie rozumiem

ss: parzystość lub nieparzystość tej funkcji. I mam jeszcze jeden przykład:

	π
f(x) = sin(		− x) i też niewiem jak tu sprawdzić parzystość bądź nieparzystość.
	2

Mila:

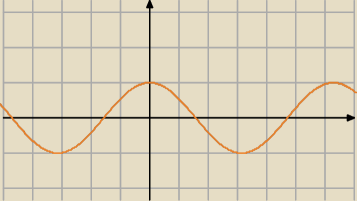
	π
f(x)=sin(		−x)=cosx funkcja parzysta− wykres jest symetryczny względem OY
	2

ss:

	π
a skąd wiedziałeś/aś Mila, że sin (		− x ) = cosx?
	2

ss: ja to muszę robić obliczeniami: I jest tak:

	π
f(x) = sin(		− x)
	2

	π		π		π		π
f(−x) = sin(		−(−x)) = sin(		+ x) =||| sin( π − (		+ x) ) = sin(		− x) =
	2		2		2		2

f(x) f(−x) = f(x) − f. parzysta. Od momentu gdzie jest: ||| − nie rozumiem.

Mila: To podstawowa zależność, w trygonometrii. Poczytaj wzory. 1) Możesz też obliczyć ze wzoru sin(α−β)=sinαcosβ−sinβcosα

	π		π		π
sin(		−x)= sin		cosx − sinx cos		=1*cosx−sinx *0=cosx
	2		2		2

2) albo możesz narysować wykres, stosując przekształcenia wykresu y=sinx

ss: 1) a mógł/mogła byś mi wypisać te najważniejsze zależności? 2) Proszę odnieś się to mojego przykładu, w sensie sposobu liczenia.

ss: pomozecie?

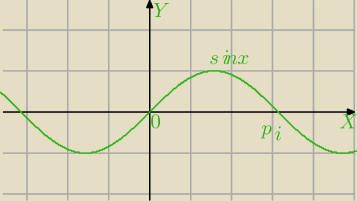
Mila: wiadomości cos(−x)=cosx funkcja parzysta wykres symetryczny względem OY sin(−x)=−sinx funkcja nieparzysta wykres symetryczny względem punkt(0;0) narysuję.

	π
f(x)=sin(		−x)=cosx
	2

	π		π		π
f(−x)=sin(		+x)=sin		cosx+sinx cos		=cosx
	2		2		2

f(x)=f(−x) f(x) jest parzysta

Mila: LO czy studia?

ss: ehhh . przerasta mnie to chyba...

	π
te wiadomosci co mi wypisałaś. ok. Ale dalej mi to nie wyjaśnia dlaczego z f(x) =sin(		−
	2

x) zrobiło się cosx...

ss: studia. ale powtarzamy materiał z liceum. a jak wiadomo nie każdy miał rozszerzoną matmę w liceum. Ja np. nie miałem. i teraz się gubię.

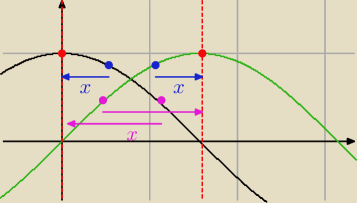
Artur_z_miasta_Neptuna: sin (90−x) = cosx ... wynika to z wykresu sinusa i cosinusa .... spójrz jak zachowuje sie sinus w przedziale od 0 do 90 ... a jak cosinus (narysuj na jednym rysunku jakie to sa studia jaki kierunek

Mila: Zobacz post 15:35 Tam zastosowałam wzór sin(α−β)= sinα*cosβ−sinβ*cosα

	π
sin		=1
	2

	π
cos		=0
	2

	π		π		π
sin(		−x)=sin		*cosx−sinx* cos		=1*cosx−0*sinx=cosx−0=cosx
	2		2		2

Zeby zrozumieć te wzory przećwicz na dobrze zrobionych przykładach. Poszukam i dam Ci linka.

	π
zrób to samo dla sin(		+x)
	2

wzór sin(α+β)= sinα*cosβ+sinβ*cosα

Mila: https://matematykaszkolna.pl/strona/3421.html Tam na początek masz wzory i przykłady.

ss: ooo i tego mi było trzeba. Wyjaśnienia. Czekam na przykłady Mila. Artur nie chce się chwalić bo narobię wstydu uczelni. Pozostawię to w tajemnicy. Natomiast moje braki wynikają z tego, że nie miałem rozszerzenia w szkole, gdzie większość je miało. I to niestety jest bardzo niesprawiedliwe, bo materiał powinien być równy.

ss: Dobra Mila. Skumałem tym sposobem ze wzorami trygo ten przykład. Dziękuje. Natomiast to rozwiązanie co podałem (15.31) jest chyba i tak jakimś innym sposobem zrobione. Prostszym. Ale niewiem jakim.

Mila: To niestety mankamenty naszego średniego szkolnictwa. Młodzi ludzie wybierają poziom podstawowy ( bo jest) a potem mają problemy. http://www.zadania.info/d62/1 równania z rozwiązaniami.

ss: A z tym(14:53) byś mi jeszcze mogła pomóc?

ss: Mila − nawet sobie nie wyobrażasz jak żałuję, ze miałem podstawową matematykę. Pluję sobie codziennie w twarz. Ale cóż, jestem po technikum. Mam zawód i słabą maturę. I teraz to będzie za mną chodzić. Przynajmniej póki powtarzamy szkołę średnią. Bo np. już liczby zespolone czy granice robię bez problemu ( te nie na poziomie hard). Bo się uczę od początku. A z tymi powtórkami czegoś czego ja nie miałem , więc właściwie to nie są dla mnie powtórki, jest ciężej.

ss: znaczy nie słabą maturę bo z podstawy miałem chyba 96 ale z rozszerza dupa. Bo nie miałem

Mila: ze wzoru redukcyjnego sin(180−α)=sinα

	π
α=		+x
	2

	π		π
sin(		+x)=sin(π−(		+x))= wykonuję w nawiasie
	2		2

	π
=sin(		−x)
	2

ss: ahaaa. no tak. bo π = 180*. Ok. to zrozumiałem jest już dla mnie.

ss: Spróbuj mi wytłumaczyć 14:53