równanie stycznej Dawid: napisać równanie prostej stycznej do paraboli y = x² − 2x + 5, równoległej do siecznej łączącej punkty o odciętych x1 = 1, x2 = 3

Basia: szkoła czy studia ? dokładniej czy można używać pochodnych czy nie ?

Dawid: studia

niepewny: a nie będzie to prosta przechodząca przez wierzchołek paraboli równoległa do osi ox?

Basia: no to szybciutko sieczna przechodzi przez punkty A=(1;f(1)) i B=(3;f(3)) f(1) = 1−2+5 = 4 f(3) = 9−6+5 = 8 czyli A(1;4) B(3;8)

	f(3)−f(1)		8−4
jej współczynnik kierunkowy m =		=		= 2
	3−1		3−1

współczynnik kierunkowy stycznej musi być taki sam f'(x) = 2x − 2 2x−2 = 2 2x = 4 x=2 czyli będzie to styczna w p−cie x₀ = 2 f(2) = 4−4+5 = 5 czyli przechodzi przez C=(2;5) równanie stycznej y = 2x+b 5 = 2*2+b b=1 y=2x+1 albo podstaw do wzoru y = f(x₀) + f'(x₀)(x−x₀) x₀=2 f(x₀) = f(2) = 5 f'(x₀) = f'(2) = 2 y = 5+2(x−2) = 2x+1

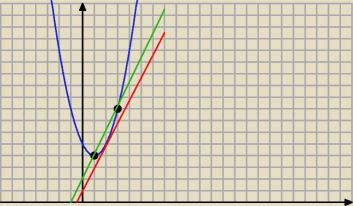
aniabb: y=2x+1